
그림 1. ‘돈룩업’ 포스터
스바루 망원경 관측소1에서 천체 사진을 보고 있는 천문 학자 케이트 디비아스키가 열심히 연구를 진행하고 있습니다. 이내 무엇인가 발견한듯 소스라치게 놀라며 소리를 지르는데요. 끝없는 관찰과 계산 끝에 그녀가 마침내 새로운 혜성을 발견했기 때문입니다. 연구실의 사람들은 새로운 혜성을 발견한 데에 있어 모두 기뻐하고 서로 축하해주지만, 이내 그 기쁨은 두려움으로 바뀌게 됩니다.
혜성의 궤도를 계산한 결과 혜성이 지구와 곧 충돌할 것이라는 결론이 나왔기 때문입니다. 영화 ‘돈 룩 업’은 지구를 향해 돌진하는 혜성의 존재를 발견한 천문학자 두 명이 혜성의 충돌에 대해 전혀 믿지 않는 지구의 사람들에게 경각심을 주기 위해 고군분투하는 내용의 영화입니다. 과연 지구의 운명은 어떻게 될까요? 오늘 공대생의 눈으로 영화보기 코너에서는 작품에서 등장한 과학적 내용에 대해 분석해보고자 합니다.
혜성의 궤도를 계산한 결과 혜성이 지구와 곧 충돌할 것이라는 결론이 나왔기 때문입니다. 영화 ‘돈 룩 업’은 지구를 향해 돌진하는 혜성의 존재를 발견한 천문학자 두 명이 혜성의 충돌에 대해 전혀 믿지 않는 지구의 사람들에게 경각심을 주기 위해 고군분투하는 내용의 영화입니다. 과연 지구의 운명은 어떻게 될까요? 오늘 공대생의 눈으로 영화보기 코너에서는 작품에서 등장한 과학적 내용에 대해 분석해보고자 합니다.
1 미국 하와이 섬의 마우나케아 천문대에 있는 일본국립천문대의 주요 망원경
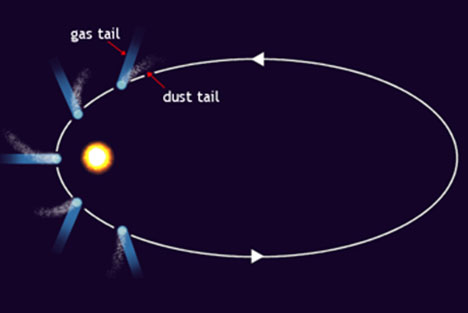
그림 2. 혜성의 모습
혜성이란 무엇일까?
영화에서는 거대한 혜성이 지구로 다가오며 사람들을 위협했는데요. 혜성이란 무엇일까요? 혜성(comet)은 태양계의 천체 중 하나로 핵과 핵을 둘러싼 코마, 먼지 꼬리, 그리고 이온 꼬리로 구성되어 있습니다. 먼저 혜성의 본체라고도 불리는 혜성의 핵은 얼음과 암석, 유기질의 먼지로 이루어져 있는데요. 핵의 평균 직경은 수백 미터 정도이고, 수십 미터부터 최대 50km까지의 크기도 가질 수 있다고 해요. 이 핵이 태양과 멀리 떨어져 있을 때는 얼어붙어 있다가, 태양과 가까워지면 태양의 복사열로 인해 핵 내부의 성분이 녹으면서 핵 주위에 가스가 생기는데요. 이 가스 대기층을 코마라고 부른답니다. 한편, 혜성은 두 종류의 꼬리를 가지고 있는데, 바로 먼지 꼬리와 이온 꼬리입니다. 혜성이 태양과 가까워져 온도가 올라가면 휘발성 물질이 승화하면서 먼지와 함께 밖으로 방출되는데요. 방출된 먼지와 휘발성 기체는 각각 먼지 꼬리와 이온 꼬리를 형성합니다. 이때 먼지 꼬리는 태양광이 반사되면서 빛이 나고, 이온 꼬리는 이온화2과정에서 빛을 내게 된답니다. 어떤가요? 혜성의 모습이 머릿속에 그려지나요?
영화에서는 거대한 혜성이 지구로 다가오며 사람들을 위협했는데요. 혜성이란 무엇일까요? 혜성(comet)은 태양계의 천체 중 하나로 핵과 핵을 둘러싼 코마, 먼지 꼬리, 그리고 이온 꼬리로 구성되어 있습니다. 먼저 혜성의 본체라고도 불리는 혜성의 핵은 얼음과 암석, 유기질의 먼지로 이루어져 있는데요. 핵의 평균 직경은 수백 미터 정도이고, 수십 미터부터 최대 50km까지의 크기도 가질 수 있다고 해요. 이 핵이 태양과 멀리 떨어져 있을 때는 얼어붙어 있다가, 태양과 가까워지면 태양의 복사열로 인해 핵 내부의 성분이 녹으면서 핵 주위에 가스가 생기는데요. 이 가스 대기층을 코마라고 부른답니다. 한편, 혜성은 두 종류의 꼬리를 가지고 있는데, 바로 먼지 꼬리와 이온 꼬리입니다. 혜성이 태양과 가까워져 온도가 올라가면 휘발성 물질이 승화하면서 먼지와 함께 밖으로 방출되는데요. 방출된 먼지와 휘발성 기체는 각각 먼지 꼬리와 이온 꼬리를 형성합니다. 이때 먼지 꼬리는 태양광이 반사되면서 빛이 나고, 이온 꼬리는 이온화2과정에서 빛을 내게 된답니다. 어떤가요? 혜성의 모습이 머릿속에 그려지나요?
2 전기적으로 중성인 입자가 양 또는 음의 전하를 띄는 현상
그렇다면 혜성은 어디서 오는 것일까요? 태양계를 돌고 있는 대부분의 혜성은 크게 두 곳에서 기원하는 것으로 알려져 있습니다. 바로 카이퍼대(Kuiper belt)와 오르트 구름(Oort could)인데요. 먼저 해왕성 너머에 위치하고 있는 카이퍼대는 암석이나 얼음으로 이루어진 작은 천체들이 얇은 원반의 형태로 모여 있는 곳으로, 태양에서 대략 45억km에서 75억km 정도 떨어져 있습니다.
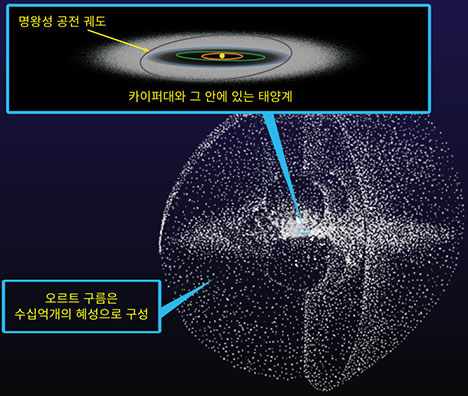
그림 3. 카이퍼대와 오르트 구름
카이퍼대를 구성하고 있는 소천체들은 태양계가 형성되었을 때부터 있었는데요. 크기가 작아 행성으로 성장하지 못한 소천체들이 충돌하고 또 서로 모이며 지금의 카이퍼대를 이루었다고 해요. 이곳의 혜성은 태양계의 행성과 동일한 방향으로 공전한다고 합니다.
또한 오르트 구름은 무작위 방향으로 공전하는 혜성들이 모여있을 것이라는 네덜란드의 과학자 얀 오르트의 가설에 의해 등장한 구형의 혜성 구름입니다. 대략 태양과 3000억km정도 떨어져 있다고 해요. 아직은 오르트 구름의 형성 과정이 정확히 규명되지 않아 그 존재가 가설에 그치고 있지만, 대부분의 과학자들은 암석이 뭉치며 행성과 소행성을 형성하는 과정에서 목성의 강한 중력으로 인해 밀쳐진 물체들이 모여 오르트 구름을 형성하였을 것이라고 예측하고 있어요. 이렇게 무작위적으로 튕겨나간 혜성은 카이퍼대의 혜성보다는 비교적 자유로운 궤도로 공전하고 있답니다.
또한 오르트 구름은 무작위 방향으로 공전하는 혜성들이 모여있을 것이라는 네덜란드의 과학자 얀 오르트의 가설에 의해 등장한 구형의 혜성 구름입니다. 대략 태양과 3000억km정도 떨어져 있다고 해요. 아직은 오르트 구름의 형성 과정이 정확히 규명되지 않아 그 존재가 가설에 그치고 있지만, 대부분의 과학자들은 암석이 뭉치며 행성과 소행성을 형성하는 과정에서 목성의 강한 중력으로 인해 밀쳐진 물체들이 모여 오르트 구름을 형성하였을 것이라고 예측하고 있어요. 이렇게 무작위적으로 튕겨나간 혜성은 카이퍼대의 혜성보다는 비교적 자유로운 궤도로 공전하고 있답니다.
천체의 운동을 설명하는 3가지 법칙, 케플러 법칙
영화에서는 혜성의 궤도를 예측하기 위해 랜달 민디 박사와 그의 조교 케이트 디비아스키가 궤도 역학의 이론을 사용하는 장면이 등장합니다. 그들은 케플러 법칙을 이용해 계산을 진행해 나갔는데요. 여기서 케플러 법칙이란, 독일의 천문학자 요하네스 케플러가 발표한 행성의 운동에 대한 물리학 법칙입니다. 케플러 법칙에는 총 3가지 법칙이 있고, 그 내용은 다음과 같습니다.
제1법칙(타원 궤도의 법칙): 행성의 공전 궤도는 타원 모양이다. 태양은 타원의 두 초점 중 하나에 위치한다.
제2법칙(면적 속도 일정의 법칙): 행성과 태양을 연결하는 가상적인 선분이 같은 시간 동안 쓸고 지나가는 면적은 항상 같다.
제3법칙(조화의 법칙): 행성의 공전 주기의 제곱은 궤도의 긴 반지름의 세제곱에 비례한다.
영화에서는 혜성의 궤도를 예측하기 위해 랜달 민디 박사와 그의 조교 케이트 디비아스키가 궤도 역학의 이론을 사용하는 장면이 등장합니다. 그들은 케플러 법칙을 이용해 계산을 진행해 나갔는데요. 여기서 케플러 법칙이란, 독일의 천문학자 요하네스 케플러가 발표한 행성의 운동에 대한 물리학 법칙입니다. 케플러 법칙에는 총 3가지 법칙이 있고, 그 내용은 다음과 같습니다.
제1법칙(타원 궤도의 법칙): 행성의 공전 궤도는 타원 모양이다. 태양은 타원의 두 초점 중 하나에 위치한다.
제2법칙(면적 속도 일정의 법칙): 행성과 태양을 연결하는 가상적인 선분이 같은 시간 동안 쓸고 지나가는 면적은 항상 같다.
제3법칙(조화의 법칙): 행성의 공전 주기의 제곱은 궤도의 긴 반지름의 세제곱에 비례한다.
뉴턴은 훗날 케플러 법칙을 기반으로 질량을 가진 물체 간의 상호작용을 설명하는 만유인력의 법칙을 발견하게 되는데요. 이런 뉴턴의 발견으로 인해 케플러 법칙은 단순히 행성과 태양 사이에서만 성립하는 것이 아니라, 질량을 가진 모든 천체에서 성립하는 것으로 확장되었습니다. 예를 들어 행성과 위성, 태양과 혜성 같은 관계에서도 전부 케플러 법칙이 성립함을 알 수 있게 되었던 것이죠.
그렇다면, 케플러 법칙은 정확히 무슨 의미를 지니는 것일까요? 이번 기사에서는 특별히 혜성의 궤도와 직접적으로 관련이 있는 1법칙과 2법칙을 자세히 알아보도록 합시다. 먼저 1법칙부터 살펴볼까요? 케플러가 말한 타원 궤도는 다음과 같은 수식으로 표현할 수 있습니다.
$r=\frac{\alpha}{1+\varepsilon cos\theta}$ ······ (1)
식이 조금 복잡해 보이죠? 처음 식을 보고 이해가 되지 않는 독자 분들도 많을 것이라 생각합니다. 분명 위치를 나타내는 식이라고 하였는데, x와 y에 대한 식으로 표현되어야 하지 않을까 하는 물음 역시 따를 것이고요. 지금 말한 것처럼, 기존의 x와 y의 좌표로 물체의 위치를 표현하는 좌표계를 데카르트 좌표계(Cartesian coordinate)라고 합니다. 그런데 케플러는 데카르트 좌표계로 천체의 위치를 간단하게 표현하기 어렵다고 판단하고 새로운 좌표계를 사용하였는데요. 그것이 바로 원점과의 거리 r과 각도 $\theta$로 표현되는 극좌표계(Polar coordinate)입니다. 극좌표계는 특히 원형의 곡선의 개형을 나타낼 때 더욱 편리해지는데요. 예를 들어 단위원을 데카르트 좌표계로 나타내려면 x²+y²=1이라고 써야 하지만, 극좌표계를 이용한다면 r=1이라고만 써도 충분한 것을 알 수 있습니다. 정말 편리하죠?
그렇다면, 케플러 법칙은 정확히 무슨 의미를 지니는 것일까요? 이번 기사에서는 특별히 혜성의 궤도와 직접적으로 관련이 있는 1법칙과 2법칙을 자세히 알아보도록 합시다. 먼저 1법칙부터 살펴볼까요? 케플러가 말한 타원 궤도는 다음과 같은 수식으로 표현할 수 있습니다.
식이 조금 복잡해 보이죠? 처음 식을 보고 이해가 되지 않는 독자 분들도 많을 것이라 생각합니다. 분명 위치를 나타내는 식이라고 하였는데, x와 y에 대한 식으로 표현되어야 하지 않을까 하는 물음 역시 따를 것이고요. 지금 말한 것처럼, 기존의 x와 y의 좌표로 물체의 위치를 표현하는 좌표계를 데카르트 좌표계(Cartesian coordinate)라고 합니다. 그런데 케플러는 데카르트 좌표계로 천체의 위치를 간단하게 표현하기 어렵다고 판단하고 새로운 좌표계를 사용하였는데요. 그것이 바로 원점과의 거리 r과 각도 $\theta$로 표현되는 극좌표계(Polar coordinate)입니다. 극좌표계는 특히 원형의 곡선의 개형을 나타낼 때 더욱 편리해지는데요. 예를 들어 단위원을 데카르트 좌표계로 나타내려면 x²+y²=1이라고 써야 하지만, 극좌표계를 이용한다면 r=1이라고만 써도 충분한 것을 알 수 있습니다. 정말 편리하죠?
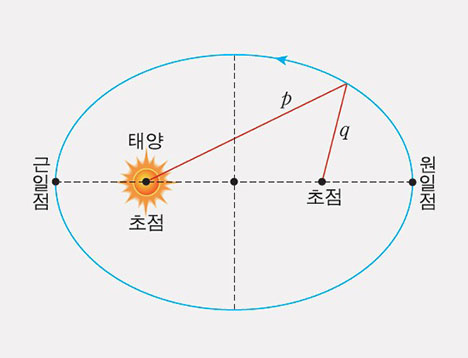
그림 4. 케플러 1법칙
그렇다면 이제 식 1을 다시 한번 살펴봅시다. 식 1과 같은 꼴은 극좌표계에서 타원의 형태를 나타내는데요, $\alpha$는 타원의 통경(latus rectum), $\varepsilon$은 타원의 이심률(orbital eccentricity)을 의미하는 값입니다. 통경은 초점에서 대칭축에 수직하게 그어 타원과 만나는 직선의 길이이고, 이심률은 곡선이 얼마나 원에 가까운지를 나타내는 값으로 0에 가까울수록 원에 가까운 형태를 띄게 됩니다. 중요한 것은 이 $\alpha$와 $\varepsilon$ 값을 찾음으로써 천체의 궤도를 수학적으로 기술할 수 있다는 것이죠. 만약 실제로 혜성을 발견하게 된다면, 이를 바탕으로 혜성의 궤도를 예측할 수 있답니다. 한 가지 영화와 다른 점은, 혜성이 지구를 향해 날아오는 과정에서 태양 외의 다른 천체들에 의한 섭동3을 받으며 궤도가 계속해서 변화하기 때문에 혜성을 발견한 즉시 지구와의 충돌 여부를 알아내기는 힘들다는 것입니다. 현실에서는 혜성을 오랜 시간 관측하면서 계산을 반복하여 궤도를 조금씩 수정하고, 관측 오차와 섭동 오차를 반영한 충돌 확률만을 알아낼 수 있다고 해요.
3 여러 개의 다른 천체로부터 중력을 받는 천체의 복잡한 움직임을 설명할 때 쓰는 용어
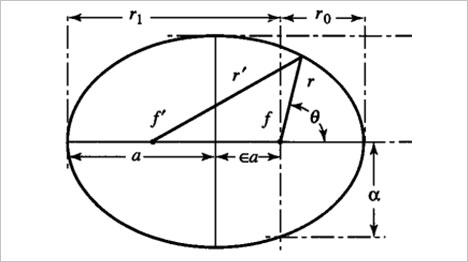
그림 5. 타원의 모습
다음으로 다룰 내용은 케플러 2법칙입니다. 설명하기 전에, 케플러 2법칙의 기본적 배경이 되는 새로운 개념을 정의하고 갈 필요가 있는데요, 바로 각운동량입니다. 각운동량이란 태양주위를 도는 혜성이나, 빠르게 도는 팽이까지 모든 회전하는 물체에서 발생하는 물리량이에요. 각운동량은 세가지 요소에 따라 그 크기가 결정되는데, ①회전하는 중심에서 멀리 떨어질수록, ②회전하는 물체가 무거울수록, ③빠르게 회전할수록 그 크기가 커진답니다. 이를 식으로 표현하면 다음과 같습니다.
L은 물체의 각운동량, m은 질량, r은 회전하는 중심으로부터의 거리, v는 속력, ω는 각속도를 의미합니다. 각속도라는 단어가 생소하게 들리실 독자분들도 있으실 텐데요. 말그대로 각도가 변하는 정도(rad/s 또는 deg/s), 즉 회전하는 빠르기를 의미한답니다.
그렇다면 각운동량 보존 법칙을 이용해 케플러 2법칙을 어떻게 설명할 수 있을까요? 앞서 케플러 1법칙을 통해 혜성은 타원궤도를 따라 공전함을 알게 되었습니다. 타원은 원과 달리 시간이 지남에 따라 태양과의 거리가 계속 달라지고, 태양과 가장 멀리 떨어진 지점을 원일점, 태양과 가장 가까운 지점을 근일점이라고 합니다. 그렇다면 이 정보를 각운동량 식에 적용해 볼까요? 혜성의 질량은 일정하므로 L이 일정하다면 거리 r과 속력 v는 반비례해야 합니다. 그렇기 때문에 혜성이 원일점일 때는 속력이 느리고, 근일점일 때는 속력이 빨라지는데요, 이것이 바로 케플러 2법칙이 의미하는 바입니다.
그렇다면 각운동량 보존 법칙을 이용해 케플러 2법칙을 어떻게 설명할 수 있을까요? 앞서 케플러 1법칙을 통해 혜성은 타원궤도를 따라 공전함을 알게 되었습니다. 타원은 원과 달리 시간이 지남에 따라 태양과의 거리가 계속 달라지고, 태양과 가장 멀리 떨어진 지점을 원일점, 태양과 가장 가까운 지점을 근일점이라고 합니다. 그렇다면 이 정보를 각운동량 식에 적용해 볼까요? 혜성의 질량은 일정하므로 L이 일정하다면 거리 r과 속력 v는 반비례해야 합니다. 그렇기 때문에 혜성이 원일점일 때는 속력이 느리고, 근일점일 때는 속력이 빨라지는데요, 이것이 바로 케플러 2법칙이 의미하는 바입니다.
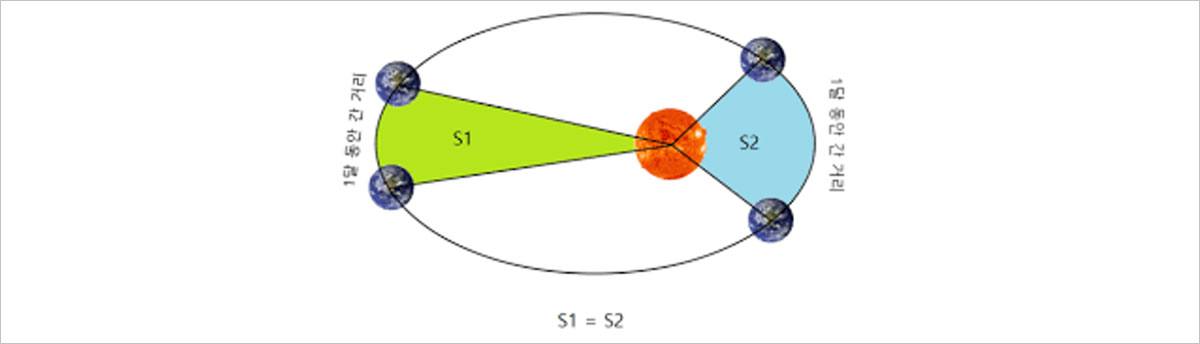
그림 6. 케플러 2법칙
실제로 혜성이 충돌한다면 무슨 일이 벌어질까?
그렇다면 실제로 혜성이 지구와 충돌할 경우 무슨 일이 벌어질까요? 또한, 어느 정도의 피해가 발생할지 어떻게 계산할 수 있을까요? 당연하게도 이를 정확히 예측하려면 정교한 시뮬레이션이 필요합니다. 하지만 이번 기사에는 복잡한 계산은 뒤로하고, 상대속도와 공전하는 천체의 에너지를 이용하여 간단하게 계산한 혜성의 위력을 살펴보겠습니다.
그렇다면 실제로 혜성이 지구와 충돌할 경우 무슨 일이 벌어질까요? 또한, 어느 정도의 피해가 발생할지 어떻게 계산할 수 있을까요? 당연하게도 이를 정확히 예측하려면 정교한 시뮬레이션이 필요합니다. 하지만 이번 기사에는 복잡한 계산은 뒤로하고, 상대속도와 공전하는 천체의 에너지를 이용하여 간단하게 계산한 혜성의 위력을 살펴보겠습니다.
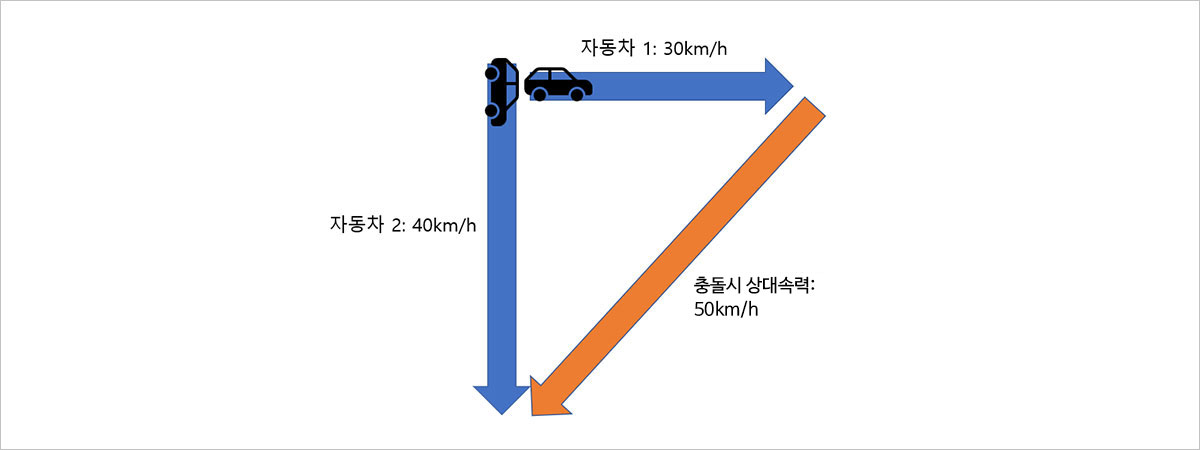
그림 7. 상대 속도의 개념
두 물체가 충돌할 때의 상대속도는 벡터를 이용한다면 쉽게 구할 수 있는데요. 벡터란 크기와 방향을 가지는 물리량으로, 여기서는 자동차의 속도를 나타냅니다. 주로 벡터는 화살표로 표현하는데, 상대속도란 한 쪽에서 본 다른 쪽의 속도이므로 두 벡터를 빼는 것과 같습니다. 벡터의 뺄셈은 한 벡터의 끝점을 다른 쪽 벡터의 시작점과 이어주면 되는데요. 그렇게 생긴 화살표의 크기와 방향이 곧 상대속도의 크기와 방향이랍니다. 두 물체가 충돌 후 서로 달라붙어 같이 움직이는 경우, 충돌에너지는 다음과 같이 표현됩니다.
$E=\frac{1}{2}\frac{m_1m_2}{m_1+m_2}v^2······(3)$
여기서 m1 ,m2는 각각 충돌하는 물체의 질량, v는 상대 속도의 크기입니다. 또한 $\frac{m_1m_2}{m_1+m_2}$는 두 물체의 환산질량(reduced mass)라고도 불린답니다. 또한 높이 있는 물체가 퍼텐셜 에너지를 가지듯이 태양의 중력에 구속 되어있는 천체들도 퍼텐셜 에너지를 가지는데요. 그 값은 다음과 같습니다.
$U=-\frac{GMm}{r}······(4)$
여기서 G는 중력상수, M, m은 각각 태양, 천체의 질량, r은 태양과 천체의 거리를 나타낸답니다. 이 값에 천체의 운동에너지를 더해주면 비로소 역학적 에너지를 구할 수 있는데요,
$E=\frac{1}{2}mv^2-\frac{GMm}{r}······(5)$
로 표현됩니다. 물체의 역학적 에너지는 보존된다는 점, 알고 계시죠? 그렇기 때문에 혜성과 태양의 거리가 바뀌면 혜성의 속력 역시 바뀌게 된답니다.
앞서 우리는 혜성이 날아오는 곳이 카이퍼대와 오르트 구름이었음을 알았습니다. 카이퍼대의 혜성은 태양계의 행성들과 동일한 공전궤도로 도는 반면, 오르트 구름에서 날아오는 혜성은 비교적 궤도가 자유로웠죠.
먼저 카이퍼대 혜성의 경우를 살펴볼까요? 그림 8을 살펴보면, 혜성이 지구와 충돌하는 경우가 크게 ①같은 방향으로 진행 ②비스듬히 진행 ③수직에 가깝게 진행하다가 충돌하는 경우로 나뉘는 것을 볼 수 있습니다. ①의 경우가 상대속도가 가장 작고, ③의 경우가 상대속도가 가장 클 것 이라고 예상이 되시죠? 그럼 이제 직접 계산을 진행해 보겠습니다. 이번 기사에서는 가장 간단한 ①의 경우만 계산해 볼게요. 먼저 영화에서 묘사한 혜성의 너비는 5~10km인데요, 혜성은 지름이 5km짜리 구 모양이고, 혜성의 밀도는 핼리 혜성의 밀도인 0.6g/cm³ 이라고 한다면 혜성의 질량은 대략 400억톤에 이릅니다. 앞서 카이퍼대에 있는 혜성이라고 하였으므로, 원일점에서 혜성과 태양의 거리는 45억km와 70억km의 평균인 60억km이라고 해봅시다. 이 혜성은 근일점에서 지구와 충돌하므로 충돌 시에는 1억5천만km까지 가까워지겠네요. 원일점에서의 혜성의 속도는 무시할 수 있다고 가정했을 때, 에너지보존법칙을 이용해 충돌 시 혜성의 속력을 구하면 다음과 같습니다.
$-\frac{G\left(4\times{10}^{13}kg\right)\left({2\times10}^{30}kg\right)}{\left(6\times{10}^{12}m\right)}=-\frac{G\left(4\times{10}^{13}kg\right)\left({2\times10}^{30}kg\right)}{\left(1.5\times{10}^{11}m\right)}+\frac{1}{2}\left(4\times{10}^{13}kg\right){v\ }^2,$
한편 지구의 공전속도는 2.98 x 10⁴m/s 이고, 같은 방향으로 공전 중이었으므로 상대 속력을 구하기 위해 두 속력 값을 빼주면 1.18 x 10⁴m/s , 즉 초속 12km입니다. 따라서 충돌 시 에너지는 다음과 같습니다.
$\frac{1}{2}\frac{\left(4\times{10}^{13}kg\right)\times\left({2\times10}^{30}kg\right)}{\left(4\times{10}^{13}kg\right)+\left({2\times10}^{30}kg\right)}\times{(1.18\times{10}^4m/s)}^2=2.78\times{10}^{21}J$
TNT 1kg의 에너지가 $4.18\times{10}^6J$이므로, 혜성이 충돌 시 발생하는 에너지는 TNT 660조 kg의 에너지와 맞먹는 것이죠.
여기서 m1 ,m2는 각각 충돌하는 물체의 질량, v는 상대 속도의 크기입니다. 또한 $\frac{m_1m_2}{m_1+m_2}$는 두 물체의 환산질량(reduced mass)라고도 불린답니다. 또한 높이 있는 물체가 퍼텐셜 에너지를 가지듯이 태양의 중력에 구속 되어있는 천체들도 퍼텐셜 에너지를 가지는데요. 그 값은 다음과 같습니다.
여기서 G는 중력상수, M, m은 각각 태양, 천체의 질량, r은 태양과 천체의 거리를 나타낸답니다. 이 값에 천체의 운동에너지를 더해주면 비로소 역학적 에너지를 구할 수 있는데요,
로 표현됩니다. 물체의 역학적 에너지는 보존된다는 점, 알고 계시죠? 그렇기 때문에 혜성과 태양의 거리가 바뀌면 혜성의 속력 역시 바뀌게 된답니다.
앞서 우리는 혜성이 날아오는 곳이 카이퍼대와 오르트 구름이었음을 알았습니다. 카이퍼대의 혜성은 태양계의 행성들과 동일한 공전궤도로 도는 반면, 오르트 구름에서 날아오는 혜성은 비교적 궤도가 자유로웠죠.
먼저 카이퍼대 혜성의 경우를 살펴볼까요? 그림 8을 살펴보면, 혜성이 지구와 충돌하는 경우가 크게 ①같은 방향으로 진행 ②비스듬히 진행 ③수직에 가깝게 진행하다가 충돌하는 경우로 나뉘는 것을 볼 수 있습니다. ①의 경우가 상대속도가 가장 작고, ③의 경우가 상대속도가 가장 클 것 이라고 예상이 되시죠? 그럼 이제 직접 계산을 진행해 보겠습니다. 이번 기사에서는 가장 간단한 ①의 경우만 계산해 볼게요. 먼저 영화에서 묘사한 혜성의 너비는 5~10km인데요, 혜성은 지름이 5km짜리 구 모양이고, 혜성의 밀도는 핼리 혜성의 밀도인 0.6g/cm³ 이라고 한다면 혜성의 질량은 대략 400억톤에 이릅니다. 앞서 카이퍼대에 있는 혜성이라고 하였으므로, 원일점에서 혜성과 태양의 거리는 45억km와 70억km의 평균인 60억km이라고 해봅시다. 이 혜성은 근일점에서 지구와 충돌하므로 충돌 시에는 1억5천만km까지 가까워지겠네요. 원일점에서의 혜성의 속도는 무시할 수 있다고 가정했을 때, 에너지보존법칙을 이용해 충돌 시 혜성의 속력을 구하면 다음과 같습니다.
한편 지구의 공전속도는 2.98 x 10⁴m/s 이고, 같은 방향으로 공전 중이었으므로 상대 속력을 구하기 위해 두 속력 값을 빼주면 1.18 x 10⁴m/s , 즉 초속 12km입니다. 따라서 충돌 시 에너지는 다음과 같습니다.
TNT 1kg의 에너지가 $4.18\times{10}^6J$이므로, 혜성이 충돌 시 발생하는 에너지는 TNT 660조 kg의 에너지와 맞먹는 것이죠.
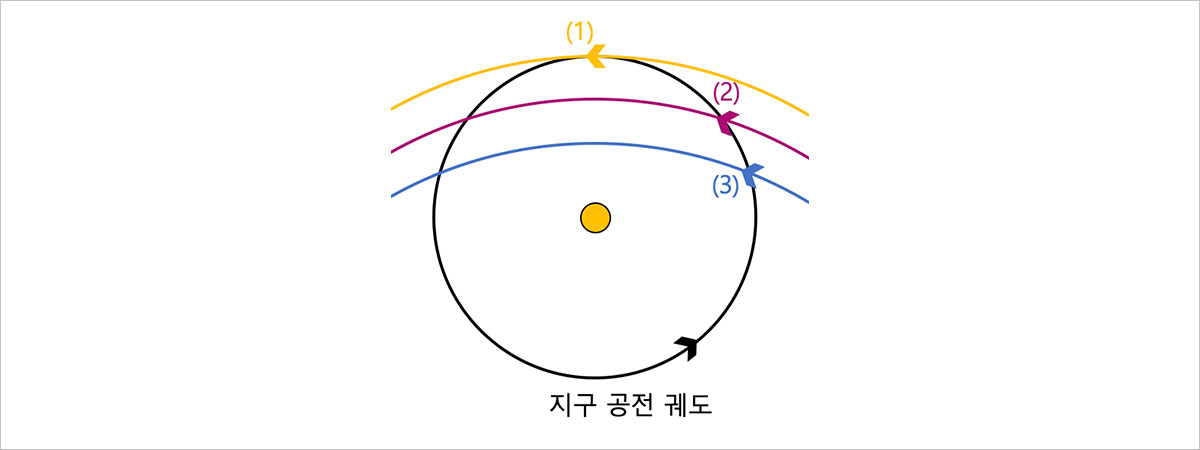
그림 8. 혜성의 충돌(카이퍼대)
그럼 이어서 오르트 구름에서 날아오는 혜성의 경우를 살펴보겠습니다. 오르트 구름에서 발생한 혜성의 궤도는 대표적으로 그림 9와 같이 두 가지가 있는데요. ①지구와 수직으로 충돌하는 궤도, ②지구와 반대 방향으로 충돌하는 궤도가 있답니다. 당연히 완벽히 반대 방향으로 충돌하는 2번 궤도가 1번 궤도보다 상대속도가 크겠죠. 마찬가지로 앞과 같은 계산 방법을 이용해, 2번 궤도의 충돌 에너지를 구해보겠습니다. 혜성이 태양과 떨어진 거리를 3천억km라고 가정한다면 지구와 혜성이 마주보는 방향으로 진행하며 충돌할 때의 혜성의 속력을 구하는 식은 다음과 같습니다.
$-\frac{G\left(4\times{10}^{13}kg\right)\left({2\times10}^{30}kg\right)}{\left(3\times{10}^{14}m\right)}=-\frac{G\left(4\times{10}^{13}kg\right)\left({2\times10}^{30}kg\right)}{\left(1.5\times{10}^{11}m\right)}+\frac{1}{2}\left(4\times{10}^{13}kg\right){v\ }^2,$
$\therefore v=4.22\times{10}^4m/s$
이번엔 반대 방향으로 충돌하는 경우이므로 지구의 공전 속력과 혜성의 충돌 속력을 더해야겠죠? 따라서 상대 속력은 7.20 x 10m⁴/s가 나오게 된답니다. 이때의 충돌 에너지는 다음과 같으며
$\frac{1}{2}\frac{\left(4\times{10}^{13}kg\right)\times\left({2\times10}^{30}kg\right)}{\left(4\times{10}^{13}kg\right)+\left({2\times10}^{30}kg\right)}\times{(7.2\times{10}^4m/s)}^2=1.04\times{10}^{23}J$
이는 TNT 2경kg의 에너지와 맞먹게 됩니다. 정말 어마어마한 양이죠?
$\therefore v=4.22\times{10}^4m/s$
이번엔 반대 방향으로 충돌하는 경우이므로 지구의 공전 속력과 혜성의 충돌 속력을 더해야겠죠? 따라서 상대 속력은 7.20 x 10m⁴/s가 나오게 된답니다. 이때의 충돌 에너지는 다음과 같으며
이는 TNT 2경kg의 에너지와 맞먹게 됩니다. 정말 어마어마한 양이죠?
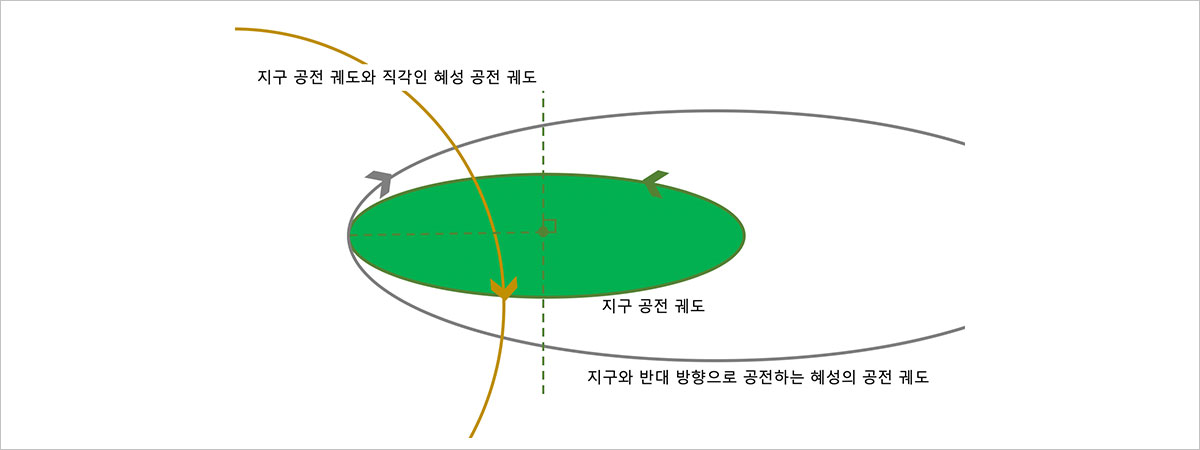
그림 9. 혜성의 충돌(오르트 구름)
이렇게 무시무시한 위력을 지닌 혜성이지만, 영화에서는 이런 혜성을 막을 시도를 하기보다는 그저 돈에 급급해 이득을 취하려는 사람들이 많이 등장합니다. 궤도를 예측한 데이터를 바탕으로 초기에 충돌을 막을 방법이 분명 있었지만, 혜성에 있는 자원을 캐고 자신들의 배를 불리기 위해 이를 계속해서 미루는 사람들의 모습을 보고 씁쓸한 기분이 들었는데요. 단순히 혜성 충돌에 대한 과학적 생각을 넘어 전 지구적 재난에서 과학자, 공학자가 가져야 할 윤리적 자세에 대해서도 생각해 볼 수 있는 유익한 영화, ‘돈 룩 업’. 독자 여러분들도 시간을 내어 한번 감상해보는 건 어떨까요?
- 참고 문헌
-
- [1] 혜성 . (n.d.). ko.wikipedia.org/wiki/%ED%98%9C%EC%84%B1
- [2] 케플러의 행성운동법칙 . (n.d.). ko.wikipedia.org/wiki/%EC%BC%80%ED%94%8C%EB%9F%AC%EC%9D%98_%ED%96%89%EC%84%B1%EC%9A%B4%EB%8F%99%EB%B2%95%EC%B9%99.
- [3] '돈 룩 업' 혜성이 실제로 지구와 충돌한다면? . (2022). ko.wikipedia.org/wiki/%EC%BC%80%ED%94%8C%EB%9F%AC%EC%9D%98_%ED%96%89%EC%84%B1%EC%9A%B4%EB%8F%99%EB%B2%95%EC%B9%99.
- 그림출처
-
그림 1. 네이버영화-‘돈 룩 업’
movie.naver.com/movie/bi/mi/photoViewPopup.naver?movieCode=192614
그림 2. 위키백과-혜성 ko.wikipedia.org/wiki/%ED%98%9C%EC%84%B1#/media/%ED%8C%8C%EC%9D%BC:Cometorbit.png
그림 3. Oort Cloud | NASA Solar System Exploration
그림 4. Mblogthumb-phinf.pstatic.net/MjAxODA0MDRfMTM4/MDAxNTIyODMwNzY4MjEy.Z05YONqzMF4OzQS_buTVp9Iwd6xbMenTqRdhUL51e4Ig.m9nFQk3rDYmK54pWQONwP1ly1wf8WoCHFuWQKHwhMXAg.JPEG.logoseduplay/2018_04_04_002.jpg?type=w800
그림 5. Analytical Mechanics(233p)
그림 6. 네이버블로그 www.google.com/url?sa=i&url=http%3A%2F%2Fm.blog.naver.com%2Fa4gkyum%2F220783396140&psig=AOvVaw1FTWRiFBBHCQqkfz8_Rl1m&ust=1651305310617000&source=images&cd=vfe&ved=0CAwQjRxqFwoTCIC__-bluPcCFQAAAAAdAAAAABAD


