
이렇듯 실제와 미니어처 모형을 둘러싼 물리적 현상이 다르게 나타나는 것을 공학에서는 크기 효과(Scale Effect)라고 부릅니다. 두 물체의 기하학적 모양이 같더라도, 질량과 표면적 등 여러 요소에서 차이가 나면 동역학적인 거동은 다르게 나타날 수 있습니다.
공학 전반에서 크기 효과는 아주 중요한 문제입니다. 특히 선박이나 항공기를 설계할 때는 추진력을 계산하기 위해 여러 번의 모형실험을 하는데요. 엔진의 출력을 부족하게 설계하면 원하는 만큼 속도가 나오지 않고, 출력을 과도하게 설계하면 자원을 많이 낭비하게 되니 정확한 출력을 계산하는 것이 매우 중요하지요. 하지만 출력은 단순히 크기에 비례하지 않습니다. 작은 규모의 모형은 파도 한 번에도 거칠게 흔들리지만 거대한 선박은 끄떡없듯이, 크기에 따라 바닷물과 상호작용하는 양상이 다르게 나타나기 때문이지요. 크기 효과를 보정하여야만 선박이나 항공기를 설계대로 제작하였을 때의 출력을 정확하게 알 수 있답니다.
19세기 영국의 공학자 윌리엄 프루드(William Froude)는 수많은 실험 끝에 모형 선박과 실제 선박의 크기 효과를 보정할 수 있는 방법을 찾아냈습니다. 영국은 프루드의 연구를 바탕으로 그들이 원하는 속도를 내는 선박을 건조할 수 있었고, 강력한 해상 군사력을 얻어 영향력을 전 세계로 확대해 나갔습니다. 공학자의 발견이 세계사의 흐름을 주도했다고 볼 수 있는 것이지요. 그의 연구에 기초하여, 오늘날에는 ‘프루드 수’라는 지표를 이용해 모형과 실제 간 크기 효과를 더욱 정확히 파악할 수 있게 되었습니다. 그럼 프루드 수로 어떻게 모형 선박의 크기 효과를 보정할 수 있는지 알아볼까요?
차원해석은 특정 물리 변수가 어떤 기본차원으로 이루어져 있는지를 파악하는 수학적 방법입니다. 이때 기본차원이란, 이들로부터 모든 물리 변수를 유도해낼 수 있는 질량(M), 길이(L), 시간(T), 전류(I), 온도(Θ), 물질량(N), 광도(J)의 7개의 독립적인 차원을 말합니다. 물리 현상이 직관적으로 잘 이해되지 않을 때, 그 현상에 관여하는 물리 변수의 차원을 분석하면 변수들 사이의 관계로부터 그 물리 현상이 어떻게 이루어지는지를 쉽게 유추해낼 수 있답니다. 예를 들어 볼까요?
자동차는 주행하면서 공기저항을 받습니다. 이 저항력은 자동차의 무슨 요소와 어떤 관계가 있는지 알아보기 위해 차원해석을 수행합시다. 우선 '공기의 저항'이라는 현상을 결정하는 후보 요인을 뽑아야 합니다. 저항력의 크기는 대략 자동차의 속도 v, 자동차의 투영 면적 A, 공기의 밀도 ρ와 관련이 있을 것 같네요.1 즉, 저항력 F를 다음과 같이 세 독립 변수의 함수로 표현할 수 있습니다.
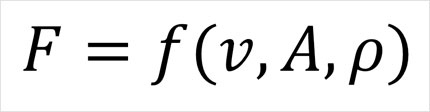
이제 F, v, A, ρ 네 변수의 차원을 살펴봅시다. 저항력은 '힘'이니까, F=ma의 관계로부터 아래와 같이 차원에 대한 식을 세울 수 있겠습니다.
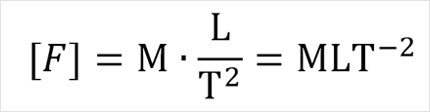
한 가지 주의할 점은, 차원분석을 할 때는 센티미터(cm)나 킬로그램(kg) 등 우리가 일상적으로 쓰는 단위는 고려하지 않고 그 물리 변수의 종류, 즉 차원만 생각해야 한다는 것입니다. 같은 방식으로 자동차 속도와 공기 밀도, 자동차 앞 유리 면적은 다음과 같이 나타낼 수 있습니다.

차원분석을 한 후 이를 수학적 모델에 적용하는 방법은 관련된 여러 물리 변수를 조합하여 모든 차원을 제거한 무차원 변수를 구하는 것입니다. 여기서 '무차원 변수'란, 물리량의 차원을 분석하고, 이를 다른 물리량들과 곱하고 나누어 물리적 차원이 없도록 만든 변수를 말합니다.
공기 저항력에 관여하는 무차원 변수를 구해 볼까요? 임의의 무차원 변수를 Π라 하면, 이는 저항력 F를 같은 차원의 변수로 나누어 차원을 제거한 형태로 구할 수 있는데요. 이때 나누는 변수는 그 차원과 같게 나머지 세 독립 변수를 조합하여 만들 수 있습니다. 수식에서 v, A, ρ 세 물리 변수가 어떤 조합으로 나누어지는지는 미지수 a, b, c를 사용해 거듭제곱 형태로 표현해야겠지요.

마지막으로 연립방정식을 세워 a, b, c를 구하면 다음과 같은 결과를 얻습니다.

1실제 유체 저항 현상에서는 유체의 점성 또한 주요한 변수로 작용하지만, 쉬운 이해를 돕기 위해 유체의 점성은 무시할 수 있다고 가정하였습니다.
결과적으로 a=-2, b=-1, c=-1임을 알 수 있습니다. 따라서 공기저항 현상에 대한 무차원 변수 Π는 다음과 같이 표현됩니다.

따라서 자동차가 받는 저항력 F는 v²ρA 에 비례한다고 할 수 있겠지요. 처음에는 저항력이라는 물리량이 어떤 요인과 어떠한 관계를 맺고 있는지 명확하지 않았지만, 차원해석과 무차원화를 통해 속도의 제곱과 유체 밀도, 그리고 투영 면적의 곱에 비례한다는 사실을 알 수 있게 된 것입니다.

가장 간단한 무차원수의 예로는 축척비가 있습니다. 무차원수인 축척비가 100,000:1인 지도가 있다고 해 봅시다. 우리나라 지도만을 보고 있었는데, 광화문에서 경복궁까지의 거리가 뉴욕 센트럴파크와 비교하여 어느 정도인지 비교할 상황이 생기면 어떻게 해야 할까요? 아무 지도나 사용한다면 실제 거리 관계를 비교하기가 쉽지 않을 것입니다. 이때 100,000이라는 숫자를 기억해 두었다가 그와 똑같은 미국 지도를 제작해 살펴보면 거리 관계를 수월하게 비교할 수 있겠지요. 이처럼 무차원수는 같은 물리 현상을 단위가 다른 상황에서 비교할 때 기준을 잡는 눈금자의 역할을 해 준다고 할 수 있습니다.
위의 경우에도 저항계수를 한 번 구해 놓으면 이후에 자동차의 속도나 공기의 밀도 등이 변화하였을 때 자동차가 받는 저항력을 손쉽게 계산할 수 있습니다. 뿐만 아니라, 동일한 기하학적 형상을 가진 물체라면 동일한 저항계수 값을 가지므로, 이를 이용하면 모형 실험의 결과를 실제 현상으로 유용하게 변환할 수 있습니다. 이처럼 차원해석과 무차원화는 여러 물리 현상을 분석함에 있어 복잡한 현상의 핵심을 알려주는 간단하면서도 매우 강력한 도구입니다.
프루드 수(Fr)는 선박이 받는 저항력에 영향을 미치는 또 하나의 무차원수입니다. 선박은 나아가면서 주위에서 형성되는 파도에 의해 저항을 받는데, 이를 조파 저항이라고 합니다. (실제 선박이 받는 저항은 점성에 의한 것이나 압력에 의한 것 등 여러 요인에 의한 것들이 있지만 프루드는 그 중 조파 저항의 영향이 가장 주요하다고 판단하였습니다.)
이 현상에는 앞선 공기 저항력의 예시와 마찬가지로 선박의 속도 v, 크기 L, 유체의 밀도 ρ이 영향을 미치게 되며, 추가적으로 파도 형성에 영향을 주는 중력가속도 g가 변수에 더해집니다.4 즉 선박이 받는 저항 R은 다음과 같이 v, L, ρ, g 네 변수의 함수로 기술할 수 있는 것이지요.
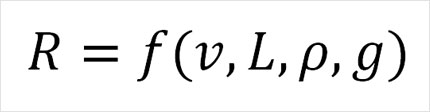
이 물리 현상에 대해 같은 방식으로 차원해석과 무차원화를 진행하면 다음 두 개의 무차원 변수 Π₁, Π₂를 얻을 수 있습니다.
2현상에 관여하는 무차원수를 1개 얻을 경우 그 무차원수를 상수라고 둘 수 있으며, 복잡한 현상에서 여러 개의 무차원수가 도출되는 경우에는 Π₁=f(Π₁, Π₂,…,Πn)와 같이 무차원수 간의 함수관계로 물리 현상을 표현할 수 있습니다. 자세한 내용이 궁금하신 분들은 ‘버킹엄 파이 정리’를 참고해 주세요!
3 정확하게는 관습적으로 2를 곱한 값인 C_d=2F/v²
ρA를 저항계수라고 정의합니다.
4여기에서 L은 선박의 크기를 대표할 수 있는 길이차원의 값으로, 일반적으로는 선박의 치수 중 수선장(Lwl, Length on waterline)이나 수선간장(Lbp, Length between perpendicular)이 사용됩니다.

즉, 선박이 받는 저항은 사실 다음과 같이 두 개 무차원수 간 함수 관계로 간단하게 표현할 수 있다는 것이죠.
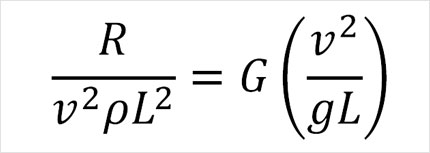
첫 번째 무차원 변수는 바로 앞에서 저항계수를 구한 동일한 방식으로 구한 선박의 저항 계수(CR)에 해당하며, 두 번째 무차원수 v²/gL의 물리적 함의를 생각해보면 이는 중력에 대한 유체저항력의 비로 유추할 수 있습니다. 앞서 유체저항력은 v²ρL²에 비례하는 형태임을 알아보았습니다. 한편 중력은 질량과 중력 가속도의 곱인데, 질량은 다시 밀도와 부피의 곱이니 gρL³로 표현할 수 있겠지요. 이 둘의 비율을 구하면 다음과 같이 두 번째 무차원 변수에 해당하는 결과를 얻을 수 있습니다.

관습적으로 저항 계수는 분모의 v²ρL² 1/2를 곱하여 계산하고, 프루드 수는 무차원 변수 v²/gL에 제곱근을 씌운 형태로 정의합니다. 따라서 이 두 변수는 다음과 같이 최종적인 형태로 쓸 수 있겠지요.


모형 선박의 경우 실험을 통해 속도와 실제 저항 값을 구할 수 있기에 역산을 통해 저항계수를 구할 수 있습니다. 그렇다면 실험을 할 수 없는 실제 선박의 저항계수는 어떻게 구해야 할까요? 저항계수는 단순히 크기나 부피에 비례하는 것이 아닙니다. 선박과 파도 사이의 상호작용, 프로펠러의 캐비테이션5 현상이 선박의 크기에 따라 천차만별로 달라지기 때문입니다. 바로 여기에서 무차원수인 프루드 수가 활용됩니다.
19세기 프루드는 여러 차례의 모형 실험을 통해 다음의 프루드 상사법칙(Law of comparison)을 알아내는 업적을 남겼습니다. “선박의 크기가 모형선 치수의 D배이고 속도 V₁, V₂, V₃⋯ 에서 측정된 모형선의 저항이 R₁, R₂, R₃⋯일 때, 실제 선박의 경우 속도 V₁√D, V₂√D, V₃√D⋯에서 R₁D³, R₂D³, R₃D³⋯ 의 저항을 받는다.” 프루드는 이 결과를 통해 모형선 저항에 대한 실험 결과를 실제 선박으로 확장시킬 수 있었고, 20세기 초 영국 해군력에 지대한 기여를 하였던 것이죠.
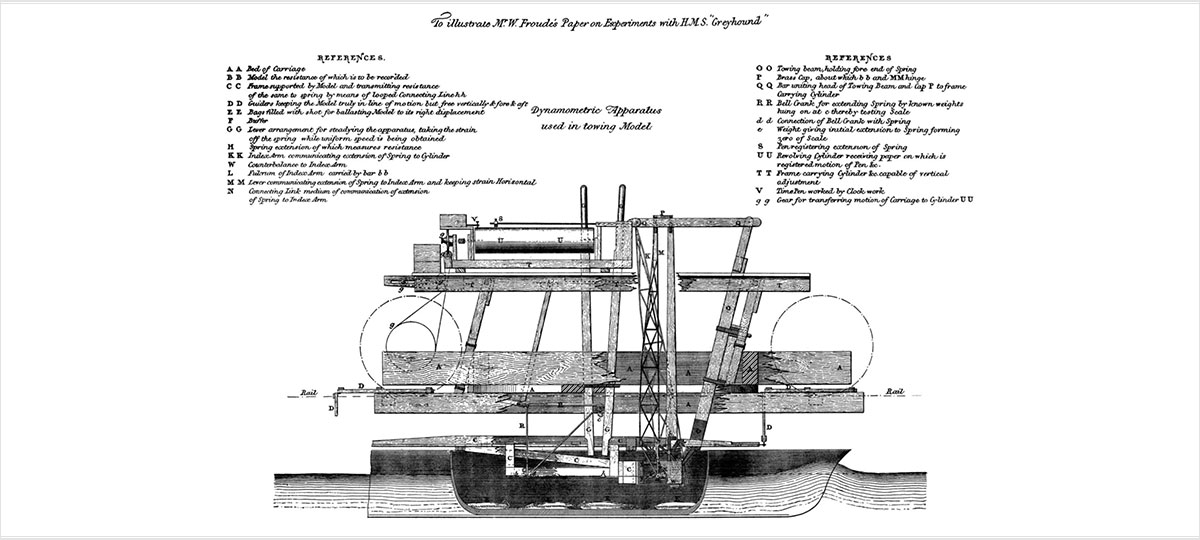
현대적 관점에서, 프루드의 연구결과는 v/√gL의 값이 같은 경우 모형과 선박의 저항계수가 일치한다는 결론으로 바라볼 수 있습니다. 예를 들어 볼까요? 총 길이가 100m인 선박이 10m/s로 운행할 때의 저항을 알아봅시다. 직접 실험할 수 없으니 25분의 1로 줄어든 4m짜리 모형을 대신 운행해 저항 계수를 알아내어야겠지요. 프루드 수가 같아지려면 크기가 1/25로 줄어들었을 때 속도는 1/5로 줄어들어야 할 것입니다. 이 모형을 2m/s로 운행하도록 하여 측정한 저항으로부터 저항계수를 구하고, 이때의 저항 계수를 실제 선박의 저항계수로 사용하면 실제 선박의 저항을 산출할 수 있습니다. 이러한 프루드의 업적을 기려, 후대 공학자들은 무차원수 v/√gL에 프루드의 이름을 붙여 부르게 된 것입니다.
이렇듯 프루드 수는 조선공학에서 선박과 다양한 요소의 상호작용을 계산해야 할 때, 실제와 모형 사이의 크기 효과를 보정하는 데에 사용됩니다. 커다란 실제 선박에서의 물리 현상을 직접 실험해 보지도 않고 모형 실험으로부터 알아낸 프루드라면, 다음과 같은 말을 하지 않았을까요?
“길고 짧은 건 안 대 봐도 안다!”
5유체의 속도가 변화할 때 압력이 변화하여 유체 내에 공기방울이 생성되는 현상
- 참고문헌
-
- [1] Fox, R. W. et al. "Fox and McDonald's Introduction to Fluid Mechanics. 8th edition." (2010).
- [2] [2] White, F. M. "Fluid mechanics/Frank M. White." (2003).
[3] Hager, Willi H., and Oscar Castro-Orgaz. "William Froude and the Froude number." Journal of Hydraulic Engineering 143.4 (2017): 02516005.
- 그림출처
-
그림 1. "24 Famous Movie Sets That Will Blow Your Mind", BuzzFeed, last modified Oct 10, (2013).
그림 2. White, F. M. "Fluid mechanics/Frank M. White." (2003).
그림 3 Hager, Willi H., and Oscar Castro-Orgaz. "William Froude and the Froude number." Journal of Hydraulic Engineering 143.4 (2017): 02516005.


