
그림 1. 윌리엄 할로우스 밀러
세상에 존재하는 거의 모든 것들은 결정 구조로 존재하고 있다고 해도 과언이 아닙니다. 얼어 있는 눈송이에서 보이는 복잡한 형태의 결정부터, 석영, 다이아몬드같이 아름다운 광물에서 관찰되는 결정까지 우리 주위에서는 참 많은 결정들을 관찰할 수 있는데요, 재료공학에서는 결정을 ‘원자의 배열이 공간 상에서 반복되는 물질’이라고 정의하고 있습니다. 아무리 커다란 물질이라도 그 속에는 반복되는 특정한 배열이 있는 것이죠.
이런 결정 구조는 우리 삶과 아주 밀접한 반도체를 만들 때 중요하게 작용합니다. 반도체의 기반이 되는 웨이퍼를 제작하는 데 실리콘(Si), 갈륨아세나이드(GaAs) 결정을 이용하고, 웨이퍼 위에 쌓아 올릴 집적회로를 만드는 공정에서도 실리콘 결정이 이용되기 때문이죠. 결정은 그 모양마다 서로 다른 특성을 가지기 때문에, 어떤 종류의 결정을 사용하였는지에 따라 반도체의 성질이 크게 좌우됩니다. 따라서 결정의 구성 형태를 알아내는 것은 반도체 산업에서 핵심 요소라고 할 수 있습니다.
이처럼 결정을 구성하는 입자의 배열, 방향 등을 사용하여 결정을 구분하는 방법은 결정학에서 매우 중요한 과정입니다. 19세기 영국의 결정학자 윌리엄 할로우스 밀러(William Hollowes Miller)는 결정 구조를 구분하기 위해 밀러지수(Miller index)라고 불리는 지표를 제시하였습니다. 밀러지수란 결정의 면과 방향을 나타내는 지수로서 결정의 구조를 기하적으로 그리지 않아도 단번에 알아볼 수 있게끔 표시하는 지수인데요, 모든 결정 구조는 이 밀러지수를 이용하여 표현할 수 있다고 합니다. 그렇다면 밀러지수란 무엇이고, 어떻게 사용하는지 한번 알아볼까요?
이런 결정 구조는 우리 삶과 아주 밀접한 반도체를 만들 때 중요하게 작용합니다. 반도체의 기반이 되는 웨이퍼를 제작하는 데 실리콘(Si), 갈륨아세나이드(GaAs) 결정을 이용하고, 웨이퍼 위에 쌓아 올릴 집적회로를 만드는 공정에서도 실리콘 결정이 이용되기 때문이죠. 결정은 그 모양마다 서로 다른 특성을 가지기 때문에, 어떤 종류의 결정을 사용하였는지에 따라 반도체의 성질이 크게 좌우됩니다. 따라서 결정의 구성 형태를 알아내는 것은 반도체 산업에서 핵심 요소라고 할 수 있습니다.
이처럼 결정을 구성하는 입자의 배열, 방향 등을 사용하여 결정을 구분하는 방법은 결정학에서 매우 중요한 과정입니다. 19세기 영국의 결정학자 윌리엄 할로우스 밀러(William Hollowes Miller)는 결정 구조를 구분하기 위해 밀러지수(Miller index)라고 불리는 지표를 제시하였습니다. 밀러지수란 결정의 면과 방향을 나타내는 지수로서 결정의 구조를 기하적으로 그리지 않아도 단번에 알아볼 수 있게끔 표시하는 지수인데요, 모든 결정 구조는 이 밀러지수를 이용하여 표현할 수 있다고 합니다. 그렇다면 밀러지수란 무엇이고, 어떻게 사용하는지 한번 알아볼까요?
결정계와 브라베 격자
밀러지수를 알아보기 전, 결정 구조가 정확히 무엇인지 짚고 넘어갈 필요가 있습니다. 앞서 결정이란 원자의 배열이 공간적으로 반복되는 패턴을 가지는 물질이라고 정의하였습니다. 패턴이 있다면 반복되는 가장 작은 단위가 있고, 우리는 이를 격자(lattice)라고 부릅니다. 그렇다면 이런 격자는 어떻게 존재하는 걸까요?
결정과 그것을 이루는 입자들은 삼차원 공간에 존재하고, 이러한 입자들을 이어 만든 격자도 삼차원 공간을 구성하게 됩니다. 그렇다면 격자는 임의의 삼차원 단위 공간에 존재하는 반복 패턴이라고 설명할 수 있어요. 여기서 말하는 ‘삼차원 단위 공간’이란, 단순히 xyz좌표계처럼 직교하면서 각 선분의 길이가 동일한 정육면체 공간만을 의미하는 것은 아닙니다. x축과 y축이 60도의 각도를 이루어 더 좁아질 수도 있고, 120도의 각도를 이루어 더욱 넓어질 수도 있습니다. x축의 단위길이와 y축의 단위길이가 서로 다를 수도 있죠. 이처럼 특정한 공간을 그것이 가진 대칭성에 따라 분류한 것을 ‘결정계’라고 합니다. 격자는 바로 이 결정계 안에 존재해요.
밀러지수를 알아보기 전, 결정 구조가 정확히 무엇인지 짚고 넘어갈 필요가 있습니다. 앞서 결정이란 원자의 배열이 공간적으로 반복되는 패턴을 가지는 물질이라고 정의하였습니다. 패턴이 있다면 반복되는 가장 작은 단위가 있고, 우리는 이를 격자(lattice)라고 부릅니다. 그렇다면 이런 격자는 어떻게 존재하는 걸까요?
결정과 그것을 이루는 입자들은 삼차원 공간에 존재하고, 이러한 입자들을 이어 만든 격자도 삼차원 공간을 구성하게 됩니다. 그렇다면 격자는 임의의 삼차원 단위 공간에 존재하는 반복 패턴이라고 설명할 수 있어요. 여기서 말하는 ‘삼차원 단위 공간’이란, 단순히 xyz좌표계처럼 직교하면서 각 선분의 길이가 동일한 정육면체 공간만을 의미하는 것은 아닙니다. x축과 y축이 60도의 각도를 이루어 더 좁아질 수도 있고, 120도의 각도를 이루어 더욱 넓어질 수도 있습니다. x축의 단위길이와 y축의 단위길이가 서로 다를 수도 있죠. 이처럼 특정한 공간을 그것이 가진 대칭성에 따라 분류한 것을 ‘결정계’라고 합니다. 격자는 바로 이 결정계 안에 존재해요.
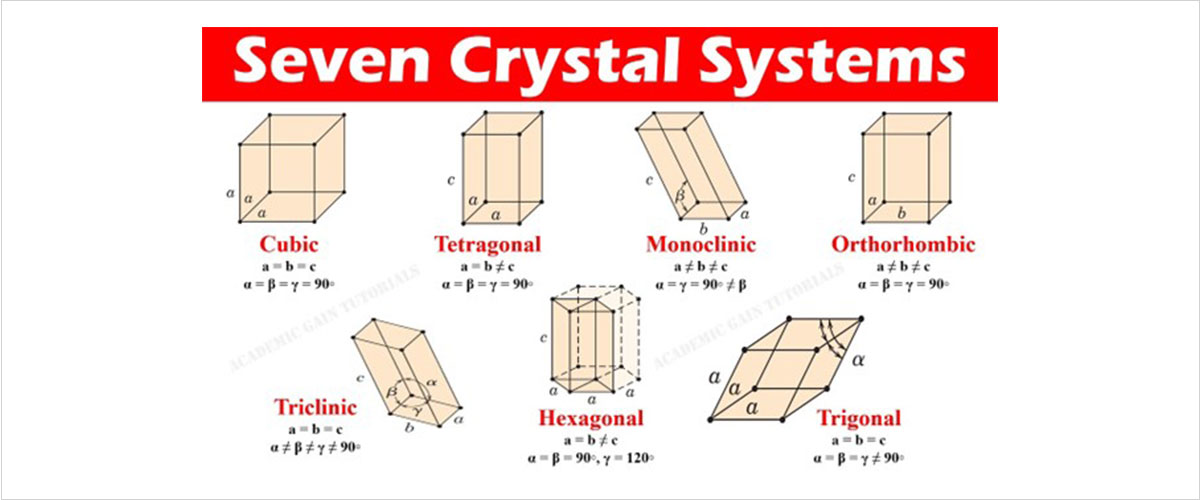
그림 2. 결정계의 모습(왼쪽부터 입방정계, 정방정계, 단사정계, 사방정계, 삼사정계, 육방정계, 삼방정계)

그림 3. 귀스트 브라베
결정계는 입방정계(cubic), 정방정계(Tetragonal), 단사정계(monoclinic), 사방정계(orthorhombic), 삼사정계(Triclinic), 육방정계(hexagonal), 삼방정계(Trigonal), 총 7가지로 구분됩니다.
입방정계는 우리가 흔히 알고 있는 정육면체 형태이고, 육방정계는 육각기둥 형태입니다.
정방정계는 밑면은 정사각형이지만 높이의 길이는 다른 직육면체 형태이고, 삼방정계는 정육면체를 비스듬하게 눕힌 형태입니다.
사방정계는 세변의 길이가 모두 다른 직육면체 형태이고, 단사정계는 사방정계를 비스듬하게 눕힌 형태입니다.
마지막으로 삼사정계는 앞서 언급한 모든 경우에 해당되지 않는 형태로 정의합니다.
입방정계는 우리가 흔히 알고 있는 정육면체 형태이고, 육방정계는 육각기둥 형태입니다.
정방정계는 밑면은 정사각형이지만 높이의 길이는 다른 직육면체 형태이고, 삼방정계는 정육면체를 비스듬하게 눕힌 형태입니다.
사방정계는 세변의 길이가 모두 다른 직육면체 형태이고, 단사정계는 사방정계를 비스듬하게 눕힌 형태입니다.
마지막으로 삼사정계는 앞서 언급한 모든 경우에 해당되지 않는 형태로 정의합니다.
그렇다면 단순히 이 7가지의 경우가 격자의 전부일까요? 결정계는 대칭성을 가지는 가장 ‘기초적인’ 단위일 뿐, 모든 결정 구조를 설명하지는 못합니다. 가령 위의 그림 중 입방정계(Isometric)에서 모든 면의 중심에 격자점을 추가하여도 이는 대칭성을 여전히 가지고, 가장 단순한 단위이기 때문에 격자의 성격을 만족합니다. 따라서 어떤 결정계에는 자기 자신의 모습과 동일한 격자뿐만 아니라 격자점을 추가하여 파생된 격자 역시 존재합니다. 격자점을 추가하는 방법은 총 네 가지인데, 기존의 결정계인 단순, 결정계의 중심에 격자점을 놓는 체심, 결정계의 면에 격자점을 놓는 면심, 윗면과 아랫면에 격자점을 추가하는 저심이 있습니다. 그렇다면 결정계의 개수가 7개이고, 각각의 가짓수가 4개이므로 28개가 되어야 하지만, 몇몇의 경우는 대칭성을 만족하지 못해 격자가 될 수 없습니다. 프랑스의 물리학자 오귀스트 브라베(Auguste Bravais)는 대칭성 조건을 만족하는 14개의 격자를 찾아 정리하였는데, 이를 브라베 격자(Bravais lattice)라고 부릅니다.
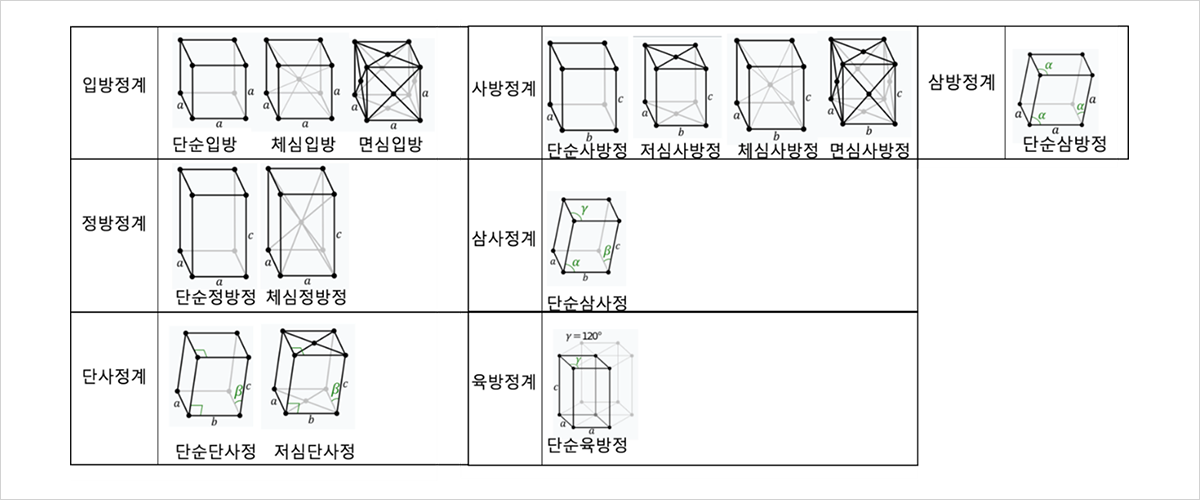
그림 4. 브라베 격자의 종류
여기서 입방정계의 브라베 격자를 살펴보면 우리가 화학시간에 배운 결정 구조와 비슷한 모습을 찾아볼 수 있습니다. 단순입방, 면심입방, 체심입방이 바로 그것이죠. 결국 다양한 결정 구조들이 브라베 격자에 속해있는 셈이랍니다.
정리하자면, 결정 구조란 특정한 결정계에서 정의되는 브라베 격자로 반복되는 패턴인 것입니다.
정리하자면, 결정 구조란 특정한 결정계에서 정의되는 브라베 격자로 반복되는 패턴인 것입니다.
브라베 격자의 결정면을 수학으로! 밀러지수
지금까지 브라베 격자에 대해 설명한 이유는 바로 밀러지수가 브라베 격자의 결정면을 설명하기 위해 등장한 수치이기 때문입니다. 밀러지수는 (hkl)꼴의 세 개, 혹은 (hkil)꼴의 네 개 숫자로 이루어져 있는데, 각 면이 어떤 방향을 향하는지에 대한 정보를 담고 있는 밀러지수 만으로도 결정면의 형태를 유추할 수 있게 되었습니다. 한 번 같이 알아볼까요?
밀러지수를 정하는 첫 번째 단계는 우선 결정면이 축과 만나는 점부터 원점까지의 길이의 역수를 구하는 것입니다. 아래의 경우 선분의 길이가 2, 3, 6이므로 역수를 구하게 되면 1/2, 1/3, 1/6이 될 것입니다.
지금까지 브라베 격자에 대해 설명한 이유는 바로 밀러지수가 브라베 격자의 결정면을 설명하기 위해 등장한 수치이기 때문입니다. 밀러지수는 (hkl)꼴의 세 개, 혹은 (hkil)꼴의 네 개 숫자로 이루어져 있는데, 각 면이 어떤 방향을 향하는지에 대한 정보를 담고 있는 밀러지수 만으로도 결정면의 형태를 유추할 수 있게 되었습니다. 한 번 같이 알아볼까요?
밀러지수를 정하는 첫 번째 단계는 우선 결정면이 축과 만나는 점부터 원점까지의 길이의 역수를 구하는 것입니다. 아래의 경우 선분의 길이가 2, 3, 6이므로 역수를 구하게 되면 1/2, 1/3, 1/6이 될 것입니다.
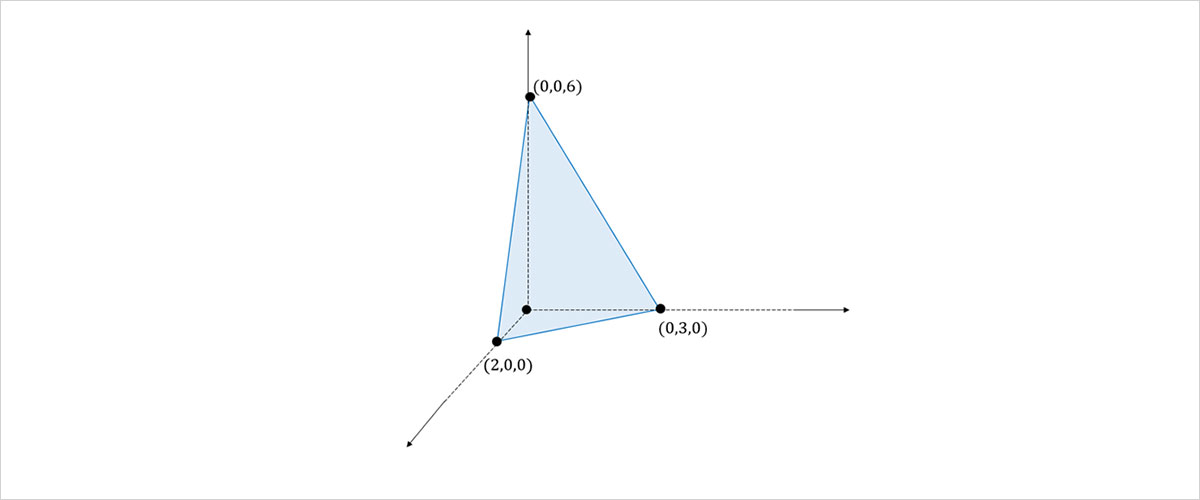
그림 5. 결정면의 모습
두 번째는 이 역수를 가장 간단한 자연수의 비로 나타내는 것입니다. 예시로 든 면의 경우 1/2 : 1/3 : 1/6 = 3 : 2 : 1이 되는데, 이를 밀러지수 형태로 표기하면 (hkl)=(321)입니다. 만약 음수가 있다면 숫자 위에 bar를 표기해 음수임을 나타냅니다. 결정면이 축과 닿지 않는 경우는 어떻게 될까요? 이 때는 선분의 길이를 무한(∞)이라고 생각할 수 있으므로 그의 역수인 0이라고 표기한답니다.
밀러지수는 단순히 숫자쌍에 불과한 것은 아니에요. 입방정계의 밀러지수는 결정면의 법선벡터를 의미합니다. 법선벡터란 평면에 수직한 벡터인데, 평면은 그 평면 위의 모든 선분과 수직인 직선이 반드시 존재합니다. 여러분 앞의 책상 위에 연필을 꼿꼿이 세워보세요. 책상 위에 어느 선을 그어도 연필이 가리키는 방향과 수직인 것을 알 수 있습니다. 이때 책상면의 법선벡터는 연필의 방향이라고 표현할 수 있는 것이죠. 즉 밀러지수가 (321)인 경우, 원점에서 점 (3,2,1)으로 향하는 방향인 벡터 (3,2,1)은 위의 결정면에 수직인 방향이 된다는 것입니다. 이제 밀러지수만 보아도 결정면이 어떤 방향을 향하고 있는지 쉽게 알 수 있겠죠?
밀러지수는 단순히 숫자쌍에 불과한 것은 아니에요. 입방정계의 밀러지수는 결정면의 법선벡터를 의미합니다. 법선벡터란 평면에 수직한 벡터인데, 평면은 그 평면 위의 모든 선분과 수직인 직선이 반드시 존재합니다. 여러분 앞의 책상 위에 연필을 꼿꼿이 세워보세요. 책상 위에 어느 선을 그어도 연필이 가리키는 방향과 수직인 것을 알 수 있습니다. 이때 책상면의 법선벡터는 연필의 방향이라고 표현할 수 있는 것이죠. 즉 밀러지수가 (321)인 경우, 원점에서 점 (3,2,1)으로 향하는 방향인 벡터 (3,2,1)은 위의 결정면에 수직인 방향이 된다는 것입니다. 이제 밀러지수만 보아도 결정면이 어떤 방향을 향하고 있는지 쉽게 알 수 있겠죠?
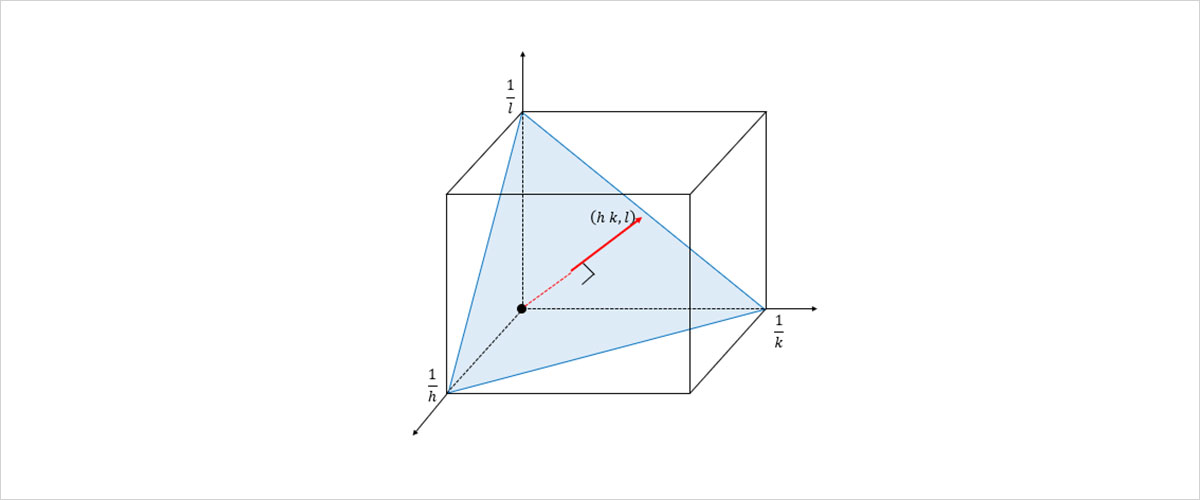
그림 6. 밀러지수로 나타낸 결정면의 법선벡터
입방정계에서의 밀러지수는 위처럼 구할 수 있었는데요, 그렇다면 육방정계에서의 밀러지수는 어떻게 구할까요? 육방정계는 입방정계와 달리 아래 그림처럼 축이 네 개인 것을 알 수 있습니다. 물론 기존의 (hkl) 표기법을 사용해 세 개의 축으로도 면의 방향을 기술할 수 있지만, 육각기둥의 대칭성이라는 기하적 특성을 나타내기 위해 바닥면에 한 개의 축을 더 추가하여 네 개의 축으로 기술하고, (hkil)으로 표기하는 것이 일반적입니다. 따라서 아래 그림의 결정면의 밀러지수는 (112 ̅0)과 같이 표현되는 것이죠.
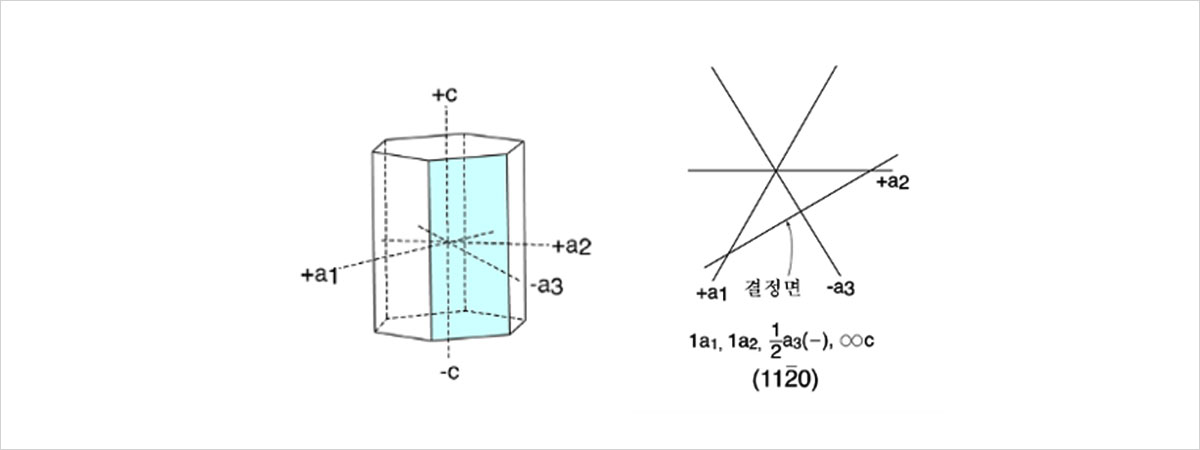
그림 7. 육방정계에서 밀러지수. 오른쪽 그림은 육각기둥 위에서 결정면을 본 그림.
지금까지 밀러지수를 어떻게 표기하는지에 대해 알아보았는데요, 그렇다면 실제 결정들은 어떤 모양인지 알아보고, 이를 밀러지수를 이용해 표기해볼까요?
먼저 가장 유명하지만, 또 가장 갖기 어려운 광물인 다이아몬드에 대해 알아봅시다. 다이아몬드는 대표적인 정팔면체(Octahedron) 결정입니다. 정삼각형의 결정면이 총 8개가 배치되어 있죠. 좌표가 모두 양수인 부분만 보면, 결정면이 정삼각형이기 때문에, x, y, z축과 만나는 좌표가 모두 같습니다. 따라서 이경우 밀러지수는 (111)이 되는 것이지요. 그렇다면 다른 면들은 대칭성에 의해 각각 아래와 같이 됩니다.
먼저 가장 유명하지만, 또 가장 갖기 어려운 광물인 다이아몬드에 대해 알아봅시다. 다이아몬드는 대표적인 정팔면체(Octahedron) 결정입니다. 정삼각형의 결정면이 총 8개가 배치되어 있죠. 좌표가 모두 양수인 부분만 보면, 결정면이 정삼각형이기 때문에, x, y, z축과 만나는 좌표가 모두 같습니다. 따라서 이경우 밀러지수는 (111)이 되는 것이지요. 그렇다면 다른 면들은 대칭성에 의해 각각 아래와 같이 됩니다.
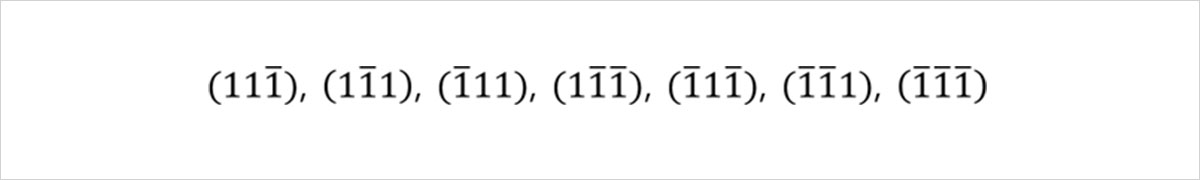
그림 8. 다이아몬드의 밀러지수
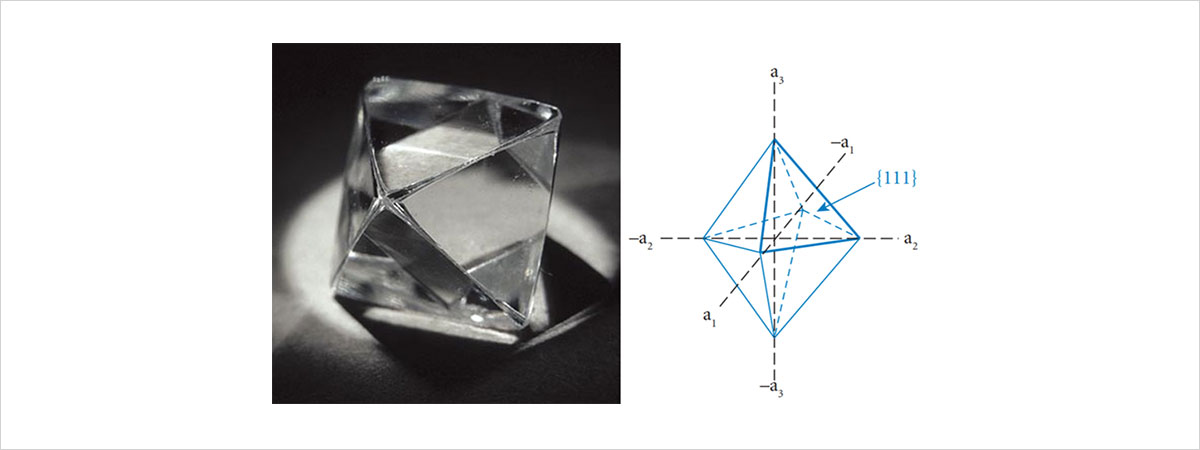
그림 9. 다이아몬드 결정의 모습-정팔면체
이번엔 시계나 라디오 같은 전자기기에 주로 사용되는 석영의 결정모습에 대해 알아보겠습니다. 석영은 육방정계의 육각 기둥(hexagonal prism)결정 구조를 가집니다. 6개의 직사각형 결정면이 정육각형을 따라 배치되어 있지요. 결정면은 밑면과 수직이기 때문에 z축과는 만나지 않고 밑면의 세개의 축과는 각각 1, 1, -1/2인 지점에서 만나는데요, 앞서 그림 7의 결정면과 같은 경우랍니다. 따라서 밀러지수 역시 (112 ̅0)로 표기하게 되고, 대칭성을 고려하여 다른 면의 밀러지수를 각각 구해주면 아래와 같습니다.

그림 10. 석영의 밀러지수
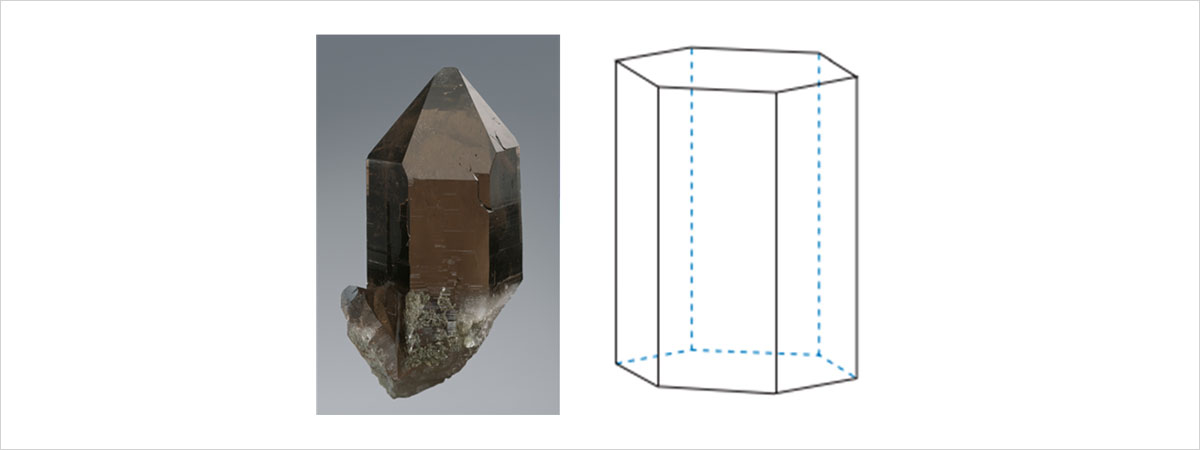
그림 11. 석영 결정의 모습-육각기둥
겉으로 보기에 별 차이가 없어 보이는 작은 조각들을 수학을 이용해 이렇게 체계적으로 분류하는 것이 진정한 과학적 사고 과정을 보여주는 듯 합니다. 기사에서 다룬 내용은 단순히 재료공학에 그치지 않고, 순수 기하학과 선형대수학에서 연구되는 분야이기도 합니다. 밀러가 연구한 결정학 내용들은 당시에 땅 속의 광물들 중 산업에 쓸모 있는 것들을 추려 공장 등에서 활용하는 데 사용되었습니다. 지금 그러한 광물들이 반도체 같은 첨단 제품들에 사용되는 모습을 보면 밀러는 얼마나 놀라워할까요? 아마도 이 한 문장으로 감상을 남기지 않을까 싶습니다.
“결정의 모습과 쓰임은 달라도 수학이 떠받치는 근본은 변함이 없다.”
“결정의 모습과 쓰임은 달라도 수학이 떠받치는 근본은 변함이 없다.”
- 그림출처
-
그림 1. https://en.wikipedia.org/wiki/William_Hallowes_Miller
그림 2. https://i.ytimg.com/vi/caStAke3F1c/maxresdefault.jpg
그림 3. https://en.wikipedia.org/wiki/Auguste_Bravais
그림 4. https://en.wikipedia.org/wiki/Miller_index
그림 7. 문희수, 최선규, 송윤구, 『광물과학』, 연세대학교 대학출판문화원(2014)
그림 9(우), 11(우). K. Hefferan and J. O’Brien, 『Earth Materials, 1st edition』, Blackwell Publishing Ltd(2010)
그림 9(좌). https://www.gia.edu/diamond-description
그림 11(좌). https://www.mindat.org/photo-265230.html (Chamosite-Clinochlore Series, eldschijen glacier, Göscheneralp, Göschenen Valley, Göschenen, Reuss Valley, Uri, Switzerland.)


