공대상상(47호)

인공지능이 우리 생활에 편의를 제공해주는 동시에, 인간 고유 영역이라고 생각돼온 예술의 영역까지 침범하고 있습니다 그 때문에 '인공지능이 사람의 능력을 뛰어넘지는 않을까?', '인공지능에 의해 일자리가 부족해지지는 않을까?' 등 우려가 종종 나오고 있습니다. 하지만, 이러한 우려가 현실화되기엔 아직 이릅니다. 대부분 인공지능은 사람이 명령하는 대로 연산을 수행하는 프로그램에 불과하지요. 지금부터 그 원리를 알아봅시다!

프랭크 로젠블렛

이번 '인물은 이렇게 말했다' 코너에서 다룰 인물은 인공지능을 연구한 미국의 신경생물학자 프랭크 로젠블렛(Frank Rosenblatt, 1928.6.11~1971.6.11)이에요. 로젠블렛은 코넬 대학교를 졸업하며, 일생동안 심리학과 인공지능 분야 연구에 매진했습니다. 로젠블렛은 인공신경망 분야에서의 연구를 인정받아 딥러닝의 아버지라 불릴 만큼 인공지능 전체의 역사에서 중요한 인물이에요.³⁾ 이번 기사에서는 인공지능 연구 초기 단계에 제안되어 후속 인공지능의 연구들에 많은 영향을 끼친 로젠블렛의 '퍼셉트론(Perceptron)'에 대해 다뤄 보도록 하겠습니다!

인공신경망

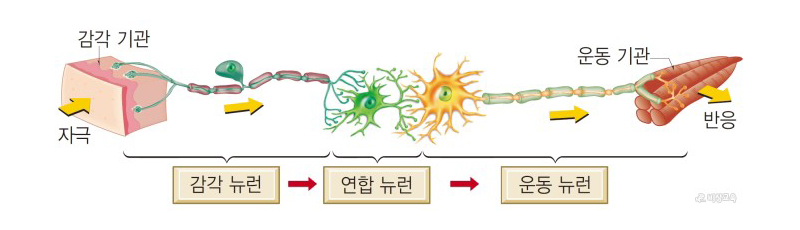
퍼셉트론을 이해하기 위해서는 먼저 인공신경망이 무엇인지 알고 있어야 해요. 인공신경망은 1943년, 신경계를 연구하던 신경과학자 워런 맥컬록(Warren McCulloch)과 월터 피츠(Walter Pitts)가 최초로 제안했습니다. 우리 신경계의 작동 방식을 아주 간단하게 도식화한다면, 그림 4와 같죠. 감각기관의 신경 수용체에서 받아들인 외부 자극은 감각 뉴런을 통해 연합 뉴런에 전달되고, 연합 뉴런이 입력된 자극에 대한 반응을 결정합니다. 이 결정은 다시 운동 뉴런을 통해 감각 기관에 전달됩니다. 그림 5에서 볼 수 있듯, 신경망은 수많은 뉴런이 얽혀 있어 매우 복잡한 형태를 가집니다. 이때 뉴런과 뉴런 사이의 공간을 시냅스라고 하는데요. 뉴런에서 뉴런으로 전기신호가 전달될 때 이 시냅스를 거쳐 전달됩니다. 그럼, 인공신경망은 우리 몸의 신경계와 어떠한 연관이 있을지 알아볼까요?⁴⁾

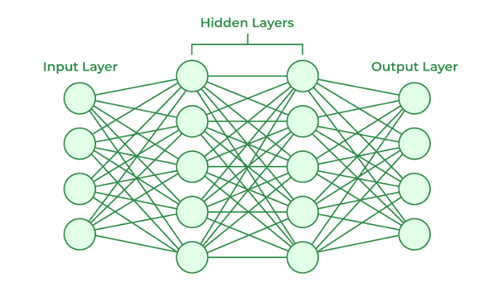
구체적인 작동 방식에는 일부 차이가 있지만, 인공신경망은 우리 몸의 신경망과 유사하게 설계되었어요. 우리 몸이 외부에서 받은 자극을 인체 내부 신경망을 통해 연합 뉴런에 전달하고 연합 뉴런의 반응을 다시 감각 기관에 전달하듯, 인공신경망도 여러 개의 데이터를 입력받은 후, 노드와 간선을 거쳐 최종적인 출력 값을 도출합니다. 외부에서 데이터를 입력받는 입력층(Input Layer)과 출력층(Output Layer)이 있고 사이에 여러 숨겨진 층(Hidden Layer)이 존재하죠. 또한, 각 층의 원 하나하나는 노드에 해당해요. 층과 층 사이는 간선들이 연결하여 마치 우리 몸의 신경계처럼 매우 복잡한 구조를 이루는 것을 알 수 있습니다. 입력된 데이터가 복잡한 구조 내부를 거쳐 가는 동안 간선에 부여된 특정한 가중치를 이용하여 사용자가 원하는 연산이 수행됩니다.

입력 값을 받아 특정한 연산 과정을 거쳐 출력 값을 도출한다는 점에서 인공신경망은 함수와 유사해 보이지만, 이 둘 사이에는 중요한 차이점이 존재합니다. 함수는 그 수식의 형태가 고정되어 있어 같은 입력 값에 대해 항상 같은 출력 값을 내는 반면, 인공신경망은 매번 층과 층 사이를 잇는 간선들에 부여된 가중치 값을 변화시키거나, 층과 간선의 연결 방식을 변화시킵니다. 이러한 내부 구조의 변화를 통해, 같은 입력 값을 넣었을 때 이전 출력 값보다 향상된 결과를 출력하지요. 이러한 과정을 '최적화'라고 부릅니다.

퍼셉트론

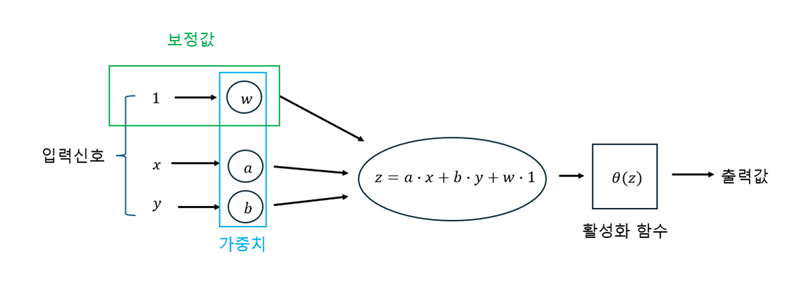
이제 인공신경망을 구체적인 수식과 알고리즘으로 최초로 표현한 예인 로젠블렛의 퍼셉트론에 대해 함께 알아볼까요? 두 가지 정보를 가진 데이터들이 있고, 우리는 이 데이터들이 어떤 그룹에 속하는지도 알고 있다고 합시다. 퍼셉트론은 이 데이터들을 이용해 학습하여 새로운 데이터가 주어졌을 때 해당 데이터가 어느 그룹에 속할지를 판단하는 알고리즘입니다. 간단한 예를 통해 살펴보도록 하겠습니다. 여러 명의 공부 시간과 몸무게 데이터가 주어졌고, 이를 통해 새로운 학생의 데이터가 입력되었을 때 '이 학생이 공부를 잘할 것인가?'라는 질문에 대한 답을 해야 하는 퍼셉트론이 있다고 해 보아요. 질문에 답하기 위해서는 우선 학생이 공부를 얼마나 잘하는지를 수치로 나타내야 합니다. 수치로 나타낼 때 퍼셉트론은 이미 주어진 데이터를 바탕으로 공부 시간과 몸무게 중 어느 것을 더 중요하게 고려할지 결정해야 해요. 여기서는 공부 시간에 더 높은 비중을 두어야 하겠죠? 즉, 퍼셉트론은 공부 시간과 몸무게 중 공부 시간에 더 높은 '가중치'를 부여하여 학생이 공부를 잘하는 정도를 예상하게 됩니다. 이를 통해 계산한 수치가 일정 수준 이상이 되면 '이 학생은 공부를 잘할 것이다'라고 판단해야 합니다. 이처럼 퍼셉트론은 특정한 값을 기준으로 학생이 공부를 잘할 확률이 이보다 더 높으면 '공부를 잘 한다', 그렇지 않으면 '공부를 잘하지 않는다'라고 이분법적으로 판별하게 되는데, 이 역할을 수행하는 함수를 '활성화 함수(Activation Function)'라고 합니다.

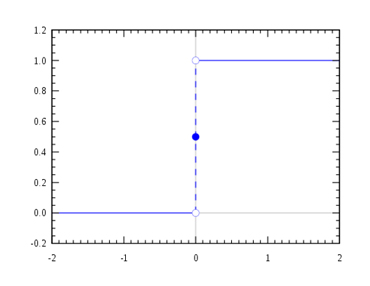
위 내용을 더 수학적으로 표현해 볼까요? x를 학생의 공부 시간, y를 학생의 몸무게라고 합시다. 그러면 입력되는 학생의 데이터를 v=(x,y)로 나타낼 수 있죠. 이제 퍼셉트론은 이 학생이 공부를 잘하는지 판별해야 합니다. x 값과 y 값 각각에 대해 적절한 가중치 a,b를 주어 학생이 공부를 잘할 확률을 계산할 수 있고, 이는 ax+by로 나타낼 수 있습니다. 이제 ax+by가 판별 기준인 p보다 큰지 작은지를 결정해야 합니다. 즉, ax+by-p의 부호를 따져주면 되죠. 여기서 p자리에 -w를 대입해주면 식이 ax+by+w=z로 더 깔끔하게 표현됩니다. 마지막으로 앞서 설명해 주었던 활성화 함수를 적용해주면 됩니다. 가장 기본적인 형태의 활성화 함수로는 z가 양수일 때는 1, 음수일 때는 0을 함숫값으로 갖는 그림 8과 같은 단위 계단 함수(Heaviside Step Function) θ가 사용됩니다. 퍼셉트론을 함수 f라고 하면 f(v)=θ(z)=θ(ax+by+w)로 최종적인 결괏값을 표현할 수 있습니다!

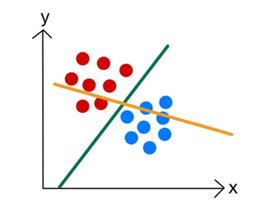
그런데 독자 여러분, 혹시 ax+by+w라는 형태의 식이 뭔가 익숙하게 느껴지지 않으시나요? 끝에 등호와 0을 붙여주게 되면, ax+by+w=0의 형태가 되어 2차원 좌표평면 위의 직선을 나타내는 식이 됩니다. 여기서 ax+by+w의 부호를 통해 점 (x,y)가 직선에 대해 위쪽, 아래쪽 중 어느 방향에 있는지 알 수 있게 됩니다. 사실 z=ax+by+w를 θ(z)에 대입한 θ(ax+by+w)는 함수에 점이 직선에 대해 어느 방향에 있는지를 판별하는 함수였던 거죠. 이처럼 퍼셉트론은 2차원 평면상의 특정한 위치에 있는 점을 입력받은 후, 그 점이 어떤 집단에 속하는지를 판별하는 판독기를 만드는 알고리즘이에요. 그림 9와 같이 2차원 평면상에 파란색과 빨간색 두 집단의 데이터가 있다고 합시다. 앞선 예시와 연결 지으면 x축과 y축의 좌표는 각각 학생의 공부 시간과 몸무게, 파란색과 빨간색 집단은 각각 공부를 잘하는 학생과 그러지 못하는 학생의 집단이 되는 것이죠.

퍼셉트론이 가중치를 찾는 과정

퍼셉트론에서 가장 중요한 부분은 두 집단을 명확하게 구분짓는 경계선을 찾는 것이죠. 그림 5의 주황색 선과 같이 두 집단을 적절히 나누지 못하는 선이 아니라 초록색 선과 같은 두 집단을 올바르게 나누는 직선을 찾는 것이 퍼셉트론의 목표예요. 직선은 가중치 a,b,w를 이용하여 표현되기 때문에 사실 적절한 a,b,w를 찾아야 합니다.

가중치를 찾는 과정을 간단하게 정리하면 다음과 같습니다.

• 1. 가중치 초기화: 우선 각 가중치의 값을 매우 작은 무작위 값으로 초기화합니다. 일반적으로 0으로 초기화하는 경우가 많습니다.

• 2. 퍼셉트론의 출력 값 계산: 주어진 데이터를 퍼셉트론에 제공, 데이터의 x,y 값을 이용하여 계산한 퍼셉트론의 출력 값을 받아옵니다.

• 3. 오차 계산: 그 후, 실제 데이터가 속한 그룹과 퍼셉트론이 예상한 결과를 비교하여 오차가 어느 정도인지 계산합니다.

• 4. 가중치 업데이트: 오류를 줄이기 위하여 가중치를 조정합니다.

• 5. 원하는 결과를 얻을 때까지 반복: 위 1~4까지의 과정을 모든 데이터에 대해 반복해 가며 가중치를 점진적으로 조정합니다. 이 과정은 계산된 오차가 원하는 값 이하로 작아지거나, 반복을 정해진 횟수만큼 할 때까지 계속합니다.

퍼셉트론은 위와 같이 주어진 데이터를 적절히 구분짓는 구분선을 찾기 위해 가중치를 조정하고 학습해요. 혹시 이 과정에 대해 더 자세히 알고 싶으신 분들은 'LMS 알고리즘'에 대해 찾아보시는 것을 추천드립니다!

퍼셉트론의 한계와 다층 퍼셉트론

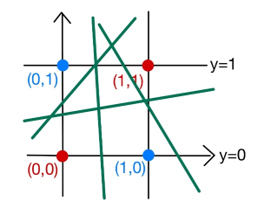
퍼셉트론은 최초로 구현된 인공지능의 형태라는 것에 의의가 있습니다. 하지만 퍼셉트론은 2차원 공간을 직선으로밖에 구분하지 못하기 때문에, 모든 집단의 경계를 완벽하게 구분할 수는 없어요. 모든 데이터의 집합들이 직선으로 명확하게 나뉘는 것은 아니기 때문이죠. 퍼셉트론이 해결하지 못하는 대표적인 예는 XOR 문제입니다. 그림 8과 같이 파란색 점 2개와 빨간색 점 2개를 좌표평면상에 배치한 경우, 경계선을 어떻게 긋더라도 두 색을 완벽하게 구분할 수 없음을 알 수 있어요.

물론 XOR 문제는 퍼셉트론이 발표된 지 얼마 지나지 않은 후, 마빈 민스키(Marvin Minsky)와 세이무르 파퍼트(Seymour Papert)가 제안한 다층 퍼셉트론(Multi-Layer Perceptron)에 의해 해결되었습니다. 로젠블렛의 퍼셉트론을 다층 퍼셉트론과 구분하기 위해 단층 퍼셉트론(Single-Layer Perceptron)이라 부르기도 하는데요. 단층 퍼셉트론은 퍼셉트론 내부의 층이 하나기 때문에 직선으로 구분 가능(Linearly separable)한 집단들에만 적용 가능했습니다. 하지만 다층 퍼셉트론은 내부에 층을 여러 개 두어 직선뿐만 아니라, 타원, 원, 2차 곡선 등 다양한 형태의 경계로 집단을 구분할 수 있기 때문에 XOR 문제를 포함한 단층 퍼셉트론이 풀지 못하는 문제들을 해결할 수 있어요. 다층 퍼셉트론 이후에도 인공지능과 인공신경망은 이미지를 분류하는 데 사용되는 CNN, 자료 분석과 패턴 인식에 이용되는 서포트 벡터 머신(Support Vector Machine) 등 다양한 분야에 적용되며 지속적으로 발전하여 오늘날의 놀라운 수준에 이르게 되었습니다.

이번 기사에서는 인공지능에서 많이 쓰이는 인공신경망의 가장 기초적인 형태인 퍼셉트론에 대해 알아보았는데요. 독자 여러분은 잘 이해가 되셨나요? 인공지능은 컴퓨터와 같이 수학적으로 설명 가능한 논리 회로에 따라 동작하도록 치밀하게 설계되어 있음을 알 수 있었습니다. 이번 기사에서 이 사실을 퍼셉트론의 원리를 뜯어 보면서 확인해 보았습니다! 물론 현재의 인공지능에는 퍼셉트론보다 더 복잡한 알고리즘이 쓰이긴 하지만, 여전히 인공지능의 설계 과정에서 수학적인 설계와 디자인이 매우 중요해요. 수학은 좋아하지만, 컴퓨터와 코딩에 대해 잘 알지 못했던 독자 여러분들도 이 기사를 읽은 후 통해 인공지능에 대해 공부하는 계기가 되었으면 좋겠습니다. 이 글을 읽은 공대상상 독자 여러분이 미래에 우리나라의 인공지능 산업을 이끌 인재가 되길 기원하며, 이번 기사는 여기서 마무리하도록 하겠습니다!