공대상상(49호)

콘슨탄틴 치올코프스키

콘스탄틴 치올코프스키(Константин Циолковский | Konstantin Tsiolkovsky, 1857~1935)는 러시아 (당시 러시아 제국~소련)의 물리학자이고, 현재 현실화된 우주정거장과 태양계 탈출의 아이디어를 제시한 인물입니다. 이에 더불어, 그는 로켓에 대한 이론을 최초로 정립했습니다. 치올코프스키는 단일 로켓이 지구 대기를 벗어나기엔 충분하지 않다는 사실을 깨닫고, 연료를 모두 소모한 단계는 분리해 버리고 새로운 단계를 점화하는 다단계 로켓의 개념을 처음으로 제안했습니다. 이 아이디어는 오늘날 로켓 기술의 핵심 원리로 사용되고 있습니다. 그가 정립한 로켓에 대한 개념을 바탕으로, 그의 이름을 딴 치올코프스키 로켓 방정식으로 다단계 로켓이 추진력을 속도를 얻어 우주로 나아갈 수 있는 원리를 수학적으로 표현했습니다.

치올코프스키 로켓 방정식

치올코프스키 로켓 방정식은 로켓의 속도 변화와 배기 가스 속도, 초기 및 최종 질량 사이의 관계를 설명하는 공식으로, 이를 통해 로켓이 속도를 높여 중력을 벗어날 수 있는 방법을 제시했습니다. 로켓은 발사가 되면 연료를 소모하면서, 추진력을 얻어 계속 앞으로 뻗어나가지만, 동시에 소모된 연료만큼 로켓의 질량이 줄어듭니다. 이 운동을 미분방정식¹⁾으로 나타낸 것이 그의 로켓 방정식입니다.

퍼텐셜이 없는 공간에서 로켓이 1차원 운동하는 경우, 초기 속도 (vⁱ), 나중 속도 (v^f), 연료 분출 속력 (u), 초기 질량 (mⁱ), 나중 질량 (m^f):

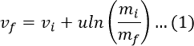
로켓이 중력장에 있을 경우:

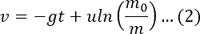
이 방정식들이 어떻게 유도 되는지 알아봅시다!

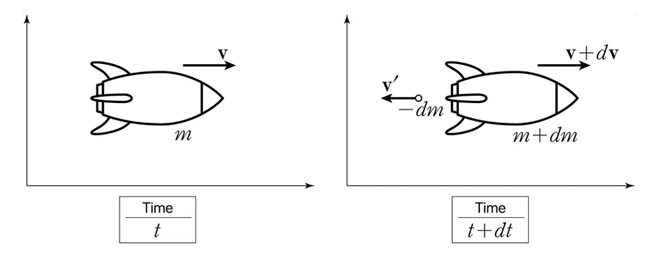
위에 사진에서는 시간 t와 t+dt일때의 로켓의 1차원 운동을 보여주고 있습니다. 우측 사진을 보면, 로켓은 연료 분출로 인한 추진력을 얻어 가속을 하게됩니다. 연료가 분충되는 방향은 로켓의 운동 방향과 평행하다고 볼 수 있습니다. 연료가 분출 된 후 로켓의 질량을 m+dm으로 정의하면, 분출되는 연료의 질량은 -dm이 됩니다. 그리고, 연료의 속력을 v'로 정의하면, 로켓의 속도는 v+dv로 표현할 수 있습니다

운동량 공식(p=mv)을 사용하면, t=t+dt에서 로켓의 운동량과 분출된 연료의 운동량을 이와 같이 표현 할 수 있습니다:

외부 힘에 대해 영향을 안받는 운동임으로, 운동량 보존 법칙을 적용하면, t일때와 t+dt일때의 운동량은 같아야 합니다:

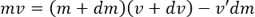
그리고 연료의 상대 속도는 -u = v' - (v + dv)이므로, -v' = u - (v + dv)를 대입 하면:

이 식을 dv에 대해 정리하면 다음과 같습니다:

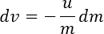
초기/나중 속도와 질량을 각각 vⁱ, v^f, mⁱ, m^f로 표현해서 적분을 적용해봅시다:

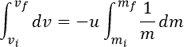
적분 후 정리를 하면 (1)번 식과 같이 나옵니다:

이제 중력장이 존재하는 경우에서 식을 유도해봅시다!

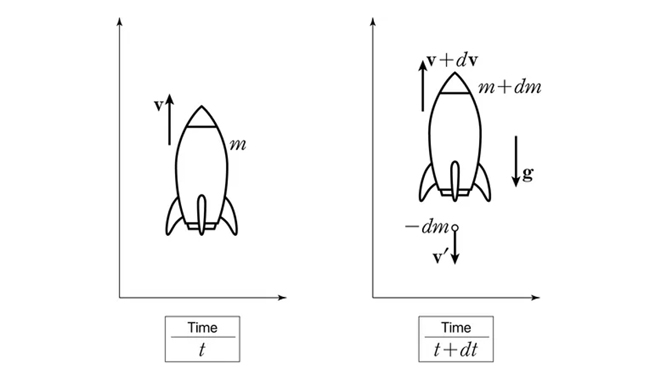
이번에도 운동량 공식을 위와 같이 똑같이 가져다가 사용하면, t에서 t+dt동안의 운동량 변화(∆p)는:

이제 충격량(Impulse)을 고려해봅시다:

위에서 사용한 연료의 상대 속도는 -u = v' - (v + dv) → -v' = u - (v + dv)를 대입해보면:

각 항들을 dt로 나눠줍니다:

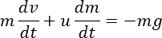
연소의 질량 변화율이 일정하다고 가정하면 (dm/dt = -c)가 성립되므로 대입을 해보면:

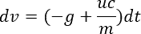
dt= -dm/c 를 대입하고 양변을 적분하면:

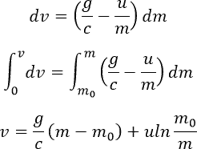
연소의 질량 변화율 (m - m0 = -ct)이므로, 대입을 해보면 (2)번과 똑같이 식이 나옵니다!

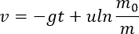
치올코프스키는 본인의 방정식을 통해 비행선이 지구의 중력장을 탈출하기 위해서는, 사용연료 대비 적재량의 비율을 높인 다단 로켓 시스템이 유리하다는것을 제시했습니다. 1번 방정식을 다시 한번 보자면:

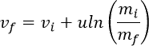
로켓의 속력(v^f)을 높이려면, mⁱ/m^f 값과 연료 분사 속도(u)값이 높아야 하는것을 알 수 있습니다. 그러나 1단 로켓이라고 가정을 하면, mⁱ, m^f값의 차이가 다단 로켓에 비해 적을 것입니다. 그러므로 mⁱ/m^f 값이 적을 것입니다. 그러나 다단 로켓은 초기에는 매우 높은 질량(mⁱ)을 가지고 있으므로 각 단계에서 연료를 다 소비하면 추진체가 분리되므로 결국 마지막 탐사선 부분이 남았을때는 초기 질량에 비해 많이 적은 질량 값을 가지고 있을거기 때문에 mⁱ/m^f값이 높을것입니다.

한국의 로켓

우리나라에서도 개발한 다단 로켓이 하나 있는데요, 바로 누리호입니다! 누리호 발사로 인해 대한민국은 자력으로 우주 로켓을 발사할 수 있는 세계 11번째 나라가 되었습니다. 이에 더해, 1톤 이상의 실용 위성을 궤도에 안착시킨 세계 7번째 나라입니다.

누리호는 총 3단 구성으로 이루어져 있습니다. 1단은 75톤급 엔진 4기로 구성되어 있으며, 2단은 75톤급 엔진 1기, 그리고 3단에는 7톤급 엔진 1기가 배치되어 있습니다. 누리호는 2021년 11월에 대망의 첫 시험 발사를 진행했으나, 아쉽게도 3단 엔진이 46초 만에 조기 종료되면서 속도 부족으로 실패로 끝났습니다. 그러나 2022년 6월에 2차 발사가 성공적으로 이루어진 덕분에 2023년 5월 25일에 실용 발사를 할 수 있었습니다. 첫 실용 발사에서 탑재 위성을 성공적으로 궤도에 안착 시키며, 첫 실용 발사는 성공적으로 마무리되었습니다. 그리고 내년 11월에 4차 발사가 예정되어 있습니다. 누리호는 한국항공우주연구원의 한국형발사체 고도화 사업의 핵심으로서, 2027년까지 작년과 내년 발사를 포함해 총 4회의 발사를 진행해서 누리호의 성능 안정성을 확인하고 민간 기업으로 발사체 기술을 이전하는 것이 계획입니다.

이번 시간에는 로켓의 아버지라고 불리는 치올코프스키가 우주과학분야에서 세운 업적을 탐구해보고 그의 로켓 방정식을 한번 유도해봤습니다. 독자 여러분들은 식 유도를 잘 따라올 수 있었나요? 물리를 좋아하거나 로켓에 관심이 있는 분들은 치올코프스키 로켓 공식을 한 번 직접 유도해보는것을 추천드립니다! 이와 더불어 치올코프스키가 제안한 이론들을 바탕으로 현재 로켓 산업과 우주공학은 어떤 방향으로 발전되고 있는지도 알아봤습니다. 여러분들은 외계 행성에서 정착할 기회가 있다면 어떻게 하실건가요? 기술이 나날이 빨리 발전하고 있는만큼, 어쩌면 우리들의 생에 인류가 우주로 진출하는 광경을 목격할 수도 있다고 생각합니다. 이 기사를 통해 독자 여러분이 항공우주공학에 관심을 가지는 계기가 되었으면 하고, 여러분들이 항공우주 산업을 빛내는 인물이 되길 바라며 이 기사는 여기서 마치도록 하겠습니다!