우리는 살면서 다양한 ‘분배’를 하게 됩니다.
친구들과 즐거운 여행을 떠난 후 여행경비를 정산할 때나, 간단한 식사 후 밥값을 계산할 때, 혹은 다 같이 진행한 프로젝트에서 보상을 받게 될 때, 우리는 분배를 생각하죠.
이처럼 우리 사회에서 분배활동은 필수적이라고 할 수 있습니다.
그렇다면 분배를 할 때 가장 중요하게 고려해야 하는 점은 무엇일까요? 바로 분배할 가치에 대한 기여도일 것입니다. 여행에서 누가 가장 돈을 많이 썼는지, 누가 가장 밥을 많이 먹었는지, 누가 프로젝트에 가장 많은 공헌을 했는지 등, 한정된 자원을 여러 사람이 나누어야 할 때는 그 자원에 대한 기여도에 따라 나누는 것이 합당하겠죠. 하지만 각자의 기여도를 수치화 하는 일은 말처럼 쉽지 않은데요, 그 이유는 여러 사람이 협력한 프로젝트에서 산출된 최종 결과물은 개인이 가지는 능력의 단순 합과는 다르기 때문입니다. 우리는 필요에 따라서 서로 협동을 하기 때문에 여기서 발생하는 시너지로 인해 더욱 결과물의 가치가 상승하게 되죠. 그렇다면 추가로 발생한 결과물의 가치를 프로젝트에 참가한 사람들의 기여도에 따라 분배하는 방법은 무엇일까요? 20세기 미국의 수학자 로이드 섀플리는 이를 해결할 수 있는 방법인 섀플리 값(Shapley Value)을 고안했는데요, 지금부터 알아봅시다!
그렇다면 분배를 할 때 가장 중요하게 고려해야 하는 점은 무엇일까요? 바로 분배할 가치에 대한 기여도일 것입니다. 여행에서 누가 가장 돈을 많이 썼는지, 누가 가장 밥을 많이 먹었는지, 누가 프로젝트에 가장 많은 공헌을 했는지 등, 한정된 자원을 여러 사람이 나누어야 할 때는 그 자원에 대한 기여도에 따라 나누는 것이 합당하겠죠. 하지만 각자의 기여도를 수치화 하는 일은 말처럼 쉽지 않은데요, 그 이유는 여러 사람이 협력한 프로젝트에서 산출된 최종 결과물은 개인이 가지는 능력의 단순 합과는 다르기 때문입니다. 우리는 필요에 따라서 서로 협동을 하기 때문에 여기서 발생하는 시너지로 인해 더욱 결과물의 가치가 상승하게 되죠. 그렇다면 추가로 발생한 결과물의 가치를 프로젝트에 참가한 사람들의 기여도에 따라 분배하는 방법은 무엇일까요? 20세기 미국의 수학자 로이드 섀플리는 이를 해결할 수 있는 방법인 섀플리 값(Shapley Value)을 고안했는데요, 지금부터 알아봅시다!

그림 1. 로이드 섀플리
로이드 섀플리
오늘 “인물을 이렇게 말했다” 코너에서 다룰 인물은 바로 미국의 수학자이자 경제학자인 로이드 스토얼 섀플리(Lloyd Stowell Shapley, 1923.6.2.~ 2016.3.12.)입니다.
섀플리는 1923년 저명한 천문학자인 할로 섀플리의 아들로 태어나 평생 수리경제학과 게임 이론 분야에서 활발한 연구를 진행했고, 그 공로를 인정받아 2012년에는 노벨 경제학상까지 수상했습니다.
특히 섀플리는 여러 사람이 협동하여 진행하는 협조적 게임이론의 창시자라고 불리는데요, 이 이론의 중심 개념이 바로 섀플리 값입니다.
오늘 “인물을 이렇게 말했다” 코너에서 다룰 인물은 바로 미국의 수학자이자 경제학자인 로이드 스토얼 섀플리(Lloyd Stowell Shapley, 1923.6.2.~ 2016.3.12.)입니다.
섀플리는 1923년 저명한 천문학자인 할로 섀플리의 아들로 태어나 평생 수리경제학과 게임 이론 분야에서 활발한 연구를 진행했고, 그 공로를 인정받아 2012년에는 노벨 경제학상까지 수상했습니다.
특히 섀플리는 여러 사람이 협동하여 진행하는 협조적 게임이론의 창시자라고 불리는데요, 이 이론의 중심 개념이 바로 섀플리 값입니다.
섀플리 값
섀플리 값(Shapley Value)이란, 어떤 프로젝트에 여러 명이 참가했을 때, 참가자들의 공헌도를 합리적이고 공정하게 나눈 값을 의미합니다. 먼저 섀플리 값을 계산할 때 가장 핵심이 되는 법칙은 다음과 같습니다. “보상의 분배는 개인이 참여한 협동의 추가적 기여와 가중치의 곱에 따라 결정된다” 추가적 기여라는 것은 무엇일까요? 추가적 기여가 발생하는 이유는 여러 사람이 협동하며 더 큰 시너지를 내기 때문입니다. 1만큼의 능력을 갖춘 사람 100명이 모이면 단순히 100이 되는 것이 아니라 1000, 10000 등 엄청난 결과물을 내놓기도 하는 것처럼 말이지요. 섀플리 값에서, 추가적 기여는 다음과 같은 식으로 계산합니다.
$V(K)-V(K/i)$
여기서 K는 특정한 협동을 의미하고, K/i는 K라는 협동에서 i번째 사람이 없을 때를 의미합니다. 또한 V는 특성함수로서, 여기서는 협동을 해서 생기는 이득을 의미합니다. 수식이 가지는 의미를 해석해보자면, 내가 포함되었을 때 얻은 이득에서 나를 제외한 나머지 사람들만 참여했을 때의 이득을 뺀 것이므로 어떤 협동에서 내가 지니는 이득 수준을 확실히 구할 수 있겠죠? 또한 가중치란 각각의 사람이 한 협동에서 가지는 비율을 의미합니다. 어떤 협동에서 발생하는 추가적 기여가 크더라도 그 협동에 참여한 사람이 많고 협동의 개수 자체도 많다면, 단순한 기여로 분배하기는 어렵겠죠? 이 때문에 추가적 기여에 협동의 중요도라는 정보를 보정해주는 수치인 가중치를 곱해주어야 한답니다.
이제 사고실험을 이용하여 직접 섀플리 값을 구해봅시다!
섀플리 값(Shapley Value)이란, 어떤 프로젝트에 여러 명이 참가했을 때, 참가자들의 공헌도를 합리적이고 공정하게 나눈 값을 의미합니다. 먼저 섀플리 값을 계산할 때 가장 핵심이 되는 법칙은 다음과 같습니다. “보상의 분배는 개인이 참여한 협동의 추가적 기여와 가중치의 곱에 따라 결정된다” 추가적 기여라는 것은 무엇일까요? 추가적 기여가 발생하는 이유는 여러 사람이 협동하며 더 큰 시너지를 내기 때문입니다. 1만큼의 능력을 갖춘 사람 100명이 모이면 단순히 100이 되는 것이 아니라 1000, 10000 등 엄청난 결과물을 내놓기도 하는 것처럼 말이지요. 섀플리 값에서, 추가적 기여는 다음과 같은 식으로 계산합니다.
여기서 K는 특정한 협동을 의미하고, K/i는 K라는 협동에서 i번째 사람이 없을 때를 의미합니다. 또한 V는 특성함수로서, 여기서는 협동을 해서 생기는 이득을 의미합니다. 수식이 가지는 의미를 해석해보자면, 내가 포함되었을 때 얻은 이득에서 나를 제외한 나머지 사람들만 참여했을 때의 이득을 뺀 것이므로 어떤 협동에서 내가 지니는 이득 수준을 확실히 구할 수 있겠죠? 또한 가중치란 각각의 사람이 한 협동에서 가지는 비율을 의미합니다. 어떤 협동에서 발생하는 추가적 기여가 크더라도 그 협동에 참여한 사람이 많고 협동의 개수 자체도 많다면, 단순한 기여로 분배하기는 어렵겠죠? 이 때문에 추가적 기여에 협동의 중요도라는 정보를 보정해주는 수치인 가중치를 곱해주어야 한답니다.
이제 사고실험을 이용하여 직접 섀플리 값을 구해봅시다!
섀플리 값 - 추가적 기여
한 프로젝트에 두 사람이 참여했다고 가정해봅시다. A는 2만큼의 능력을 발휘할 수 있고, B는 3만큼의 능력을 발휘할 수 있습니다. 이런 두 사람이 두 능력을 단순히 더한 5보다 더 높은 값인 6만큼의 결과물을 만들어냈다면, A와 B는 총 결과물인 6에서 얼만큼 기여했다고 할 수 있을까요?
이렇게 두 사람이 협동하여 진행한 경우에 대해 보상의 분배 문제를 풀어봅시다. 위 문단에 있는 공식에 따르면 V(A)=2, V(B)=3, V({A,B})=6이 되겠네요.1
그렇다면 이제 가능한 협동에 따른 추가적 기여를 계산해 봅시다. A와 B가 프로젝트를 진행하는 내내 같이 하지는 않겠죠? 어느 때는 각자 일을 할 때도 있고, 어느 날은 협동하는 경우도 있을 겁니다. 먼저 A의 경우 혼자 일을 진행하였을 때의 추가적 기여는 V(A)-V({ })=2-0=2가 됩니다.2 또한 A와 B가 일을 같이 진행한 경우 A의 추가적 기여는 V({A, B})-V(B)=6-3=3 이 됩니다. B의 경우를 살펴볼까요? 먼저 B가 혼자 일을 진행한 경우 추가적 기여는 V(B)-V( )=3-0=3, A와 B가 같이 일을 진행한 경우 B의 추가적 기여는 V({A, B})-V(A)=6-2=4가 됩니다. 표로 정리하면 협동하는 인원의 개수를 의미하는 변수인 |K|(K의 크기)에 따라 다음과 같이 나올 수 있겠네요.
한 프로젝트에 두 사람이 참여했다고 가정해봅시다. A는 2만큼의 능력을 발휘할 수 있고, B는 3만큼의 능력을 발휘할 수 있습니다. 이런 두 사람이 두 능력을 단순히 더한 5보다 더 높은 값인 6만큼의 결과물을 만들어냈다면, A와 B는 총 결과물인 6에서 얼만큼 기여했다고 할 수 있을까요?
이렇게 두 사람이 협동하여 진행한 경우에 대해 보상의 분배 문제를 풀어봅시다. 위 문단에 있는 공식에 따르면 V(A)=2, V(B)=3, V({A,B})=6이 되겠네요.1
그렇다면 이제 가능한 협동에 따른 추가적 기여를 계산해 봅시다. A와 B가 프로젝트를 진행하는 내내 같이 하지는 않겠죠? 어느 때는 각자 일을 할 때도 있고, 어느 날은 협동하는 경우도 있을 겁니다. 먼저 A의 경우 혼자 일을 진행하였을 때의 추가적 기여는 V(A)-V({ })=2-0=2가 됩니다.2 또한 A와 B가 일을 같이 진행한 경우 A의 추가적 기여는 V({A, B})-V(B)=6-3=3 이 됩니다. B의 경우를 살펴볼까요? 먼저 B가 혼자 일을 진행한 경우 추가적 기여는 V(B)-V( )=3-0=3, A와 B가 같이 일을 진행한 경우 B의 추가적 기여는 V({A, B})-V(A)=6-2=4가 됩니다. 표로 정리하면 협동하는 인원의 개수를 의미하는 변수인 |K|(K의 크기)에 따라 다음과 같이 나올 수 있겠네요.
1 {A, B}는 A와 B가 서로 협동한 경우를 의미합니다.
2 V(A/A)의 경우 A가 혼자 일을 진행하였는데 A가 없는 경우이므로 빈칸인 V({ })로 표시하고 이 값은 0입니다.

표 1. 협동에 따른 추가적 기여
섀플리 값 – 협동의 가중치
이렇게 추가적 기여까지 구해보았습니다. 이제 마지막으로 가중치를 구해서 협동의 최종 섀플리 값을 구해 봅시다. 앞서 혼자 프로젝트를 진행하는 경우, 둘이서 같이 프로젝트를 진행하는 경우로 협동을 나누어 주었는데요, 이 각각의 협동이 프로젝트에서 얼마만큼의 가중치를 가지는지 계산해야 합니다.
먼저 혼자 진행한 경우(|K|=1), 가능한 경우의 수는 A가 혼자 진행하는 경우(A)와 B가 혼자 진행하는 경우(B)로 두 가지입니다. 여기서 A의 가중치를 계산해 주면 먼저 두 가지 중에 (A)가 돼야 하므로 $\frac{1}{2}$ , (A)의 경우에서는 참여자가 A뿐이므로 $\frac{1}{1}$을 곱하여 가중치는 $\frac{1}{2}$×$\frac{1}{1}$= $\frac{1}{2}$이 됩니다. B의 가중치도 똑같이 계산하면 $\frac{1}{2}$이겠죠?
또한 둘이서 협동한 경우(|K|=2), 가능한 협동의 개수는 A와 B가 모두 진행하는 경우 한가지입니다({A, B}). 여기서 A의 가중치를 계산해 주면 우선 한 가지 상황만 가능하므로 $\frac{1}{1}$, 협동에 속해 있는 A, B 두 명 중 A가 뽑혀야 하므로 $\frac{1}{2}$을 곱하여 가중치는 $\frac{1}{1}$× $\frac{1}{2}$= $\frac{1}{2}$이 됩니다. B의 경우도 마찬가지로 $\frac{1}{2}$이 되겠네요.
이렇게 추가적 기여까지 구해보았습니다. 이제 마지막으로 가중치를 구해서 협동의 최종 섀플리 값을 구해 봅시다. 앞서 혼자 프로젝트를 진행하는 경우, 둘이서 같이 프로젝트를 진행하는 경우로 협동을 나누어 주었는데요, 이 각각의 협동이 프로젝트에서 얼마만큼의 가중치를 가지는지 계산해야 합니다.
먼저 혼자 진행한 경우(|K|=1), 가능한 경우의 수는 A가 혼자 진행하는 경우(A)와 B가 혼자 진행하는 경우(B)로 두 가지입니다. 여기서 A의 가중치를 계산해 주면 먼저 두 가지 중에 (A)가 돼야 하므로 $\frac{1}{2}$ , (A)의 경우에서는 참여자가 A뿐이므로 $\frac{1}{1}$을 곱하여 가중치는 $\frac{1}{2}$×$\frac{1}{1}$= $\frac{1}{2}$이 됩니다. B의 가중치도 똑같이 계산하면 $\frac{1}{2}$이겠죠?
또한 둘이서 협동한 경우(|K|=2), 가능한 협동의 개수는 A와 B가 모두 진행하는 경우 한가지입니다({A, B}). 여기서 A의 가중치를 계산해 주면 우선 한 가지 상황만 가능하므로 $\frac{1}{1}$, 협동에 속해 있는 A, B 두 명 중 A가 뽑혀야 하므로 $\frac{1}{2}$을 곱하여 가중치는 $\frac{1}{1}$× $\frac{1}{2}$= $\frac{1}{2}$이 됩니다. B의 경우도 마찬가지로 $\frac{1}{2}$이 되겠네요.
섀플리 값의 계산 – 2인 협동
이제 A와 B, 두 사람이 프로젝트를 진행할 때 발생하는 모든 협동에서 협동의 추가적 기여와 가중치를 구하게 되었습니다. 앞서 말했듯이 섀플리 값은 추가적 기여의 총합에 비례해야 하므로, 추가적 기여와 그 기여에 해당하는 가중치를 곱한 값을 모두 더해서 구하게 됩니다. 이제 한번 계산해봅시다!
먼저 A의 경우, A가 참여하는 협동은 총 두 가지가 있었는데요, A가 혼자 진행하는 협동과 둘이서 진행하는 협동입니다. 혼자 진행한 경우 추가적 기여는 2, 가중치는 $\frac{1}{2}$이었고, 둘이서 협동한 경우 추가적 기여는 3, 가중치는 $\frac{1}{2}$이었습니다. 따라서 A의 섀플리 값은 추가적 기여와 가중치를 더한 값인 2×$\frac{1}{2}$+3×$\frac{1}{2}$=$\frac{5}{2}$=2.5가 됩니다. B의 경우도 마찬가지로 추가적 기여와 가중치를 곱해서 구해보면 3×$\frac{1}{2}$+4×$\frac{1}{2}$=$\frac{7}{2}$=3.5가 되는 것을 확인할 수 있네요. 2.5+3.5는 6이므로, 우리는 드디어 A와 B 두 사람이 6이라는 이득을 어떻게 나눠야 할지 구해낼 수 있게 된 것입니다! 이 결과를 표로 나타내면 다음과 같이 나타낼 수 있습니다.
이제 A와 B, 두 사람이 프로젝트를 진행할 때 발생하는 모든 협동에서 협동의 추가적 기여와 가중치를 구하게 되었습니다. 앞서 말했듯이 섀플리 값은 추가적 기여의 총합에 비례해야 하므로, 추가적 기여와 그 기여에 해당하는 가중치를 곱한 값을 모두 더해서 구하게 됩니다. 이제 한번 계산해봅시다!
먼저 A의 경우, A가 참여하는 협동은 총 두 가지가 있었는데요, A가 혼자 진행하는 협동과 둘이서 진행하는 협동입니다. 혼자 진행한 경우 추가적 기여는 2, 가중치는 $\frac{1}{2}$이었고, 둘이서 협동한 경우 추가적 기여는 3, 가중치는 $\frac{1}{2}$이었습니다. 따라서 A의 섀플리 값은 추가적 기여와 가중치를 더한 값인 2×$\frac{1}{2}$+3×$\frac{1}{2}$=$\frac{5}{2}$=2.5가 됩니다. B의 경우도 마찬가지로 추가적 기여와 가중치를 곱해서 구해보면 3×$\frac{1}{2}$+4×$\frac{1}{2}$=$\frac{7}{2}$=3.5가 되는 것을 확인할 수 있네요. 2.5+3.5는 6이므로, 우리는 드디어 A와 B 두 사람이 6이라는 이득을 어떻게 나눠야 할지 구해낼 수 있게 된 것입니다! 이 결과를 표로 나타내면 다음과 같이 나타낼 수 있습니다.
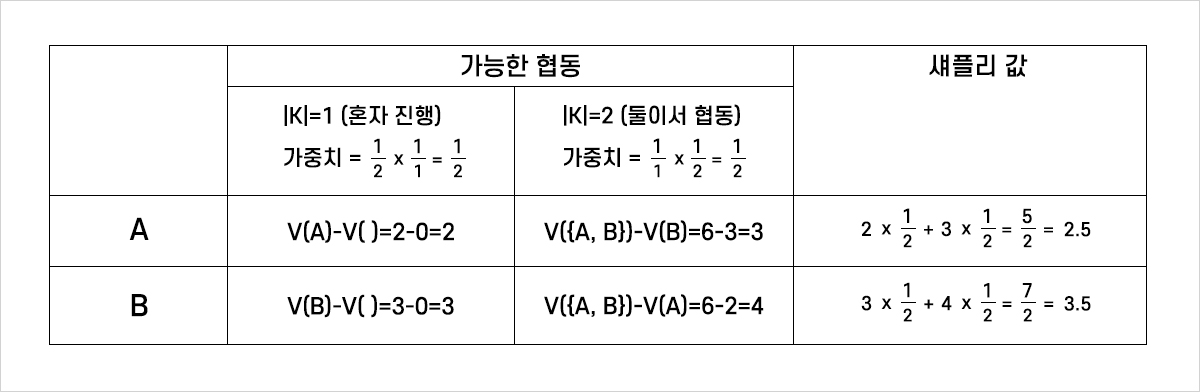
표 2. 2인 협동의 경우 섀플리 값의 계산
따라서 A와 B가 이번 프로젝트에 대한 보수로 600만 원을 받게 되었다면, A는 250만 원, B는 350만 원으로 나누어 가져야 합당한 분배가 된다는 것이지요.
수학적 계산을 통해 각 사람이 받아야 할 몫을 정확히 계산할 수 있다는 점이 신기하지 않나요?
섀플리 값의 계산 – 여러 명의 협동
만약 A, B, C 세 명이서 협동을 한 경우에는 어떻게 분배할 수 있을까요? 만약 어떤 프로젝트에서 세 명이 협동을 하게 된다면, 가능한 협동의 가짓수는 두 명일 때보다 훨씬 늘어나게 됩니다.
만약 A, B, C 세 명이서 협동을 한 경우에는 어떻게 분배할 수 있을까요? 만약 어떤 프로젝트에서 세 명이 협동을 하게 된다면, 가능한 협동의 가짓수는 두 명일 때보다 훨씬 늘어나게 됩니다.

표 3. 3인 협동의 가중치
일반적으로 N명의 사람이 협동하는 상황에서 K명이 참여할 때의 가중치를 다음과 같이 나타낼 수 있습니다.
$W_{K}=\frac{(|K|-1)!(N-|K|)!}{N!}$
또한 동일한 상황에서 추가적 기여는 앞서 언급한 식을 사용하면 쉽게 구할 수 있습니다.
$V(K)-V(K/i)$
그렇다면, N명의 사람이 협동하는 프로젝트의 경우 i번째 사람의 섀플리 값은 다음과 같은 식으로 계산할 수 있습니다.
$ SV_{i}=\sum\limits_{k} \frac{(|K|-1)!(N-|K|)!}{N!}[V(K)-V(K/i)] $
시그마 K는 i가 포함되는 모든 협동에 대해서 합을 구하겠다는 의미입니다. 또한 시그마 안의 첫 번째 항($\frac{(|K|-1)!(N-|K|)!}{N!}$)은 앞서 구한 가중치를 의미하고, 두 번째 항$([V(K)-V(K/i)])$은 추가적 기여를 의미합니다. 이제 공대상상 독자 여러분들도 단체 프로젝트를 진행한 후 각자가 프로젝트에 기여한 정도를 구해낼 수 있겠죠?
현대 사회는 ‘공조의 장’이라고 불러도 과언이 아닐 정도로, 다양한 능력을 지닌 사람들이 한데 융합해 창의적이고 유용한 공학적 산물을 만들어내고 있습니다. 하지만 이런 눈부신 성과도 개인의 공헌과 보수를 인정받아야 가능한 것이겠죠? 따라서 사람들이 가지는 가치를 수치적으로 재단하고 이에 걸맞은 분배를 하는 방법은 더욱 더 중요해지고 있습니다. 산업 공학이란 산업 시스템의 효율성을 연구하는 학문으로서, 오늘 다룬 주제인 효율적인 분배나 기업의 운영 과정에서 있어 더욱 많은 이익을 낼 수 있는 시스템 최적화에 대해 연구하는 과목인데요. 따라서 오늘 소개해드린 산업 공학적 분배 방법을 이용한다면 더욱 구성원들에게 합리적으로 보수를 나누어 줄 수 있겠죠? 공대상상 독자 여러분들도 훗날 우리나라의 공학 산업을 이끄는 리더가 되어 여러 사람들에게 합리적인 분배를 해 줄 수 있는 현명한 사람으로 거듭나길 바라면서, 이상 글을 마치겠습니다.
$W_{K}=\frac{(|K|-1)!(N-|K|)!}{N!}$
또한 동일한 상황에서 추가적 기여는 앞서 언급한 식을 사용하면 쉽게 구할 수 있습니다.
$V(K)-V(K/i)$
그렇다면, N명의 사람이 협동하는 프로젝트의 경우 i번째 사람의 섀플리 값은 다음과 같은 식으로 계산할 수 있습니다.
$ SV_{i}=\sum\limits_{k} \frac{(|K|-1)!(N-|K|)!}{N!}[V(K)-V(K/i)] $
시그마 K는 i가 포함되는 모든 협동에 대해서 합을 구하겠다는 의미입니다. 또한 시그마 안의 첫 번째 항($\frac{(|K|-1)!(N-|K|)!}{N!}$)은 앞서 구한 가중치를 의미하고, 두 번째 항$([V(K)-V(K/i)])$은 추가적 기여를 의미합니다. 이제 공대상상 독자 여러분들도 단체 프로젝트를 진행한 후 각자가 프로젝트에 기여한 정도를 구해낼 수 있겠죠?
현대 사회는 ‘공조의 장’이라고 불러도 과언이 아닐 정도로, 다양한 능력을 지닌 사람들이 한데 융합해 창의적이고 유용한 공학적 산물을 만들어내고 있습니다. 하지만 이런 눈부신 성과도 개인의 공헌과 보수를 인정받아야 가능한 것이겠죠? 따라서 사람들이 가지는 가치를 수치적으로 재단하고 이에 걸맞은 분배를 하는 방법은 더욱 더 중요해지고 있습니다. 산업 공학이란 산업 시스템의 효율성을 연구하는 학문으로서, 오늘 다룬 주제인 효율적인 분배나 기업의 운영 과정에서 있어 더욱 많은 이익을 낼 수 있는 시스템 최적화에 대해 연구하는 과목인데요. 따라서 오늘 소개해드린 산업 공학적 분배 방법을 이용한다면 더욱 구성원들에게 합리적으로 보수를 나누어 줄 수 있겠죠? 공대상상 독자 여러분들도 훗날 우리나라의 공학 산업을 이끄는 리더가 되어 여러 사람들에게 합리적인 분배를 해 줄 수 있는 현명한 사람으로 거듭나길 바라면서, 이상 글을 마치겠습니다.
- 출처
- 그림 1. https://ko.wikipedia.org/wiki/ 로이드_섀플리


