공대상상 첫 화면으로 이동

2025년의 키워드 '양자 컴퓨터'

UN은 양자역학 탄생 100주년을 기념하여 2025년을 '세계 양자 과학 기술의 해'로 지정하였습니다. 인공지능에 대한 관심이 뜨거웠던 2024년을 지나 2025년에는 양자 과학 기술에 대한 관심이 뜨거워지고 있습니다.

오늘날 양자 컴퓨팅이 주목받는 이유는 크게 두 가지입니다. 먼저, 전통적인 반도체 공정이 점차 물리적 한계에 다다르면서, 빠르게 증가하는 산업적 요구를 충족하는 것에 어려움이 있을 것이라는 예측 때문입니다. 또한 화학·재료 시뮬레이션, 금융 포트폴리오 최적화, 머신러닝 등은 고전 컴퓨터로는 사실상 불가능하거나 지나치게 오랜 시간이 걸립니다. 결국 이를 해결하려면 양자 컴퓨팅 같은 새로운 패러다임이 필요합니다.

양자 컴퓨터는 '중첩(Superposition)'과 '얽힘(Entanglement)' 같은 양자역학적 특성을 활용하여 특수한 문제에 대해 기존 컴퓨터보다 뛰어난 해결 능력을 보입니다. 2019년 구글의 시카모어(Sycamore)는 양자 컴퓨터가 현존 최고 성능 컴퓨터보다 더 뛰어난 성능을 보인다는 '양자 우위(Quantum Supremacy)'를 보이며 양자 컴퓨터 상용화에 한걸음 다가갔습니다.ⁱ⁾

양자? 중첩? 그게 무슨 개념일까요? 공대상상 44호 특집 기사 '양자역학이 바꾸는 세상'을 통해 양자 컴퓨터의 기반이 되는 양자역학에 대해 자세히 살펴보실 수 있습니다.¹⁾

비트와 큐비트

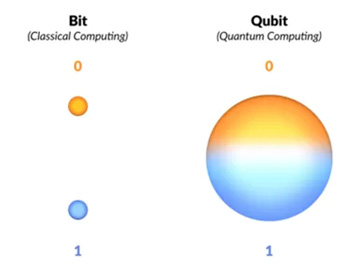
양자 컴퓨터는 기본적인 단위부터 기존 컴퓨터와 다릅니다. 기존 컴퓨터는 비트(Bit)라는 단위를 통해 연산합니다. 비트는 0 또는 1 하나의 값을 가지며 트랜지스터 전기 신호의 켜짐(1)과 꺼짐(0)을 통해 구현됩니다. 반면, 양자 컴퓨터는 0과 1을 동시에 가질 수 있는 '중첩(superposition)'의 특성을 가진 큐비트(Qubit)를 통해 연산합니다. 1개의 큐비트에는 2개의 상태가 10개의 큐비트에는 1024(2¹⁰)개의 상태가 중첩될 수 있습니다. 이렇게 중첩된 큐비트는 양자 컴퓨터가 동시에 여러 가능성을 탐색하는 기반이 됩니다.

예를 들어, 자물쇠로 잠긴 보물상자를 열 때 기존 컴퓨터라면 비밀번호 4자리를 0000부터 9999까지 하나씩 시도해야 하지만, 양자 컴퓨터는 큐비트를 이용해 10,000개의 후보(0000~9999)를 중첩 상태로 만들어 자물쇠를 풀 수 있습니다.

그러나 기존 컴퓨터도 여러 컴퓨터에서 병렬적으로 연산을 처리하거나 적절한 알고리즘을 통해 수많은 연산을 빠르게 처리할 수 있습니다. 양자 컴퓨터가 차별성을 가지는 점은 연산이 '비결정론적'이라는 점입니다.

중첩의 의미, 비결정론적 연산

"0과 1의 상태가 동일한 확률로 중첩되어 있습니다." 이 말은 얼핏 들었을 때 "존재하는 상태가 0일 확률이 1/2, 1일 확률이 1/2"이라는 뜻으로 들리기도 합니다. 하지만 분명히 0과 1이라는 상태는 관측 이전까지 모두 존재합니다. 더 정확히 말하자면, 큐비트는 관측 전까지 '두 가지 상태가 중첩되어 있는 상태' 그 자체로 존재하다가 관측되는 순간 하나의 상태로 결정되는 것입니다.

이처럼 관측되지 않은 큐비트가 비결정론적이기 때문에 양자 컴퓨터는 여러가지 결과값을 한 번에 연산할 수 있습니다. 모든 중첩된 입력에 대해 중첩된 결과가 연산된다는 점이, 한 번에 한 가지 연산을 해야 하는 결정론적인 기존 컴퓨터와 가장 큰 차별점입니다.

중첩 상태의 기술, 파동 함수

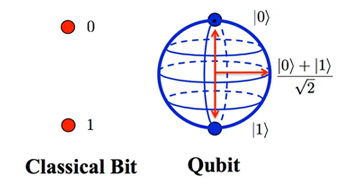
큐비트는 0과 1이라는 상태의 중첩인 파동 함수로 표현됩니다. 파동 함수는 양자역학에서 입자의 상태를 기술하는 방법으로, 입자가 가질 수 있는 모든 가능성을 포함하고 있습니다. 큐비트가 0과 1을 동시에 가진다는 것은 0과 1의 상태(∣0⟩, ∣1⟩)가 결합되어 새로운 파동 함수(∣ψ⟩)가 만들어지는 것을 의미합니다. 아래 파동 함수에서 ∣α∣2와 ∣β∣2는 각각 큐비트가 ∣0⟩과 ∣1⟩ 상태일 확률을 나타내며 그 합은 1입니다.

∣ψ⟩=α∣0⟩+β∣1⟩²⁾

이처럼 '중첩(Superposition)'이라는 양자적 특성으로 인해 양자 컴퓨터는 적은 큐비트로도 많은 상태를 표현할 수 있을 뿐 아니라 중첩된 많은 상태를 동시에 연산할 수 있습니다. 이 연산의 경우 큐비트의 상태인 파동 함수를 보강, 상쇄 간섭을 이용하여 조절할 수 있습니다. 이러한 연산을 적용할 수 있는 특수한 문제들에 대해 적절한 알고리즘이 개발된다면 양자 컴퓨터가 매우 빠르게 문제를 해결해낼 수 있습니다.

그러나 실제 구현에서는 아직 해결할 문제가 있습니다. 바로 관측에 의한 양자 붕괴입니다. .

툭하면 양자 붕괴

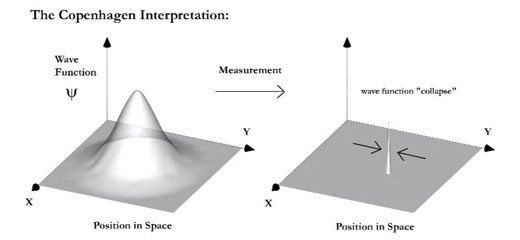
중첩된 큐비트를 관측하면 그 순간 '양자 붕괴'가 일어나 상태가 하나로 결정됩니다. 그런데 중첩 상태는 단순히 사람이 눈으로 관측해야만 붕괴하는 것이 아니라, 먼지나 공기 중의 원자 같은 외부 환경과 사소한 상호작용만으로도 쉽게 무너질 수 있습니다. 즉, 큐비트의 상태를 안정적으로 유지하려면 외부 간섭을 최소화해야 합니다. 이를 위해 다양한 구현 방식이 연구되고 있습니다. 가장 많이 연구되고 있는 초전도체 방식은 극저온에서 전기저항이 사라지는 초전도 물질을 이용해 큐비트를 구현하는 것입니다. 구글의 시카모어(Sycamore) 칩 역시 초전도체 방식을 적용한 예입니다. 이외에도 이온트랩 방식이나 광자를 이용한 방식도 연구 중입니다.

이처럼 여러 기술이 개발되고 있지만, 중요한 점은 정답을 확인하기 위해 큐비트를 관측하는 순간에도 양자 붕괴가 일어난다는 것입니다. 즉, 예시에서 자물쇠를 열기 위해 10000개의 후보가 중첩된 큐비트를 관측하는 순간 비밀번호가 1개로 결정되는 것입니다. 여기서 문제는 모든 숫자가 동일한 확률로 중첩되어 있기 때문에, 관측으로 정답을 얻을 확률이 0.01%에 불과하다는 것입니다. 즉, 기존 컴퓨터처럼 모든 후보를 시도하는 것과 큰 차이가 없어지는 셈입니다. 따라서 큐비트를 관측하지 않으면서 정답을 가려내는 방법이 필요합니다.

눈 감고 연산하기?

큐비트를 관측하지 않으면서 정답을 확인하는 것이 가능할까요? 다행히 앞선 예시의 비밀번호 중첩의 경우에는 이러한 양자 붕괴를 피하면서도 정답을 찾는 알고리즘이 존재합니다. 바로 그로버(Grover) 알고리즘입니다. 그로버 알고리즘의 개념은 앞선 공대상상 44호 특집 기사에서도 다룬 바가 있어 이번 기사에서는 조금 더 깊게 그 원리를 살펴보고자 합니다.

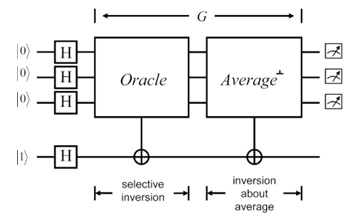
그로버 알고리즘은 '오라클(Oracle)'과 '평균 진폭 반사(Inversion about average)'라는 두 가지 주요 과정을 통해 여러 가지 상태 중 원하는 상태를 찾아내는 알고리즘입니다. 두 과정을 통해 정답 상태의 확률을 1에 충분히 가깝게 만들어서 관측 시에 높은 정확도로 정답 상태로 큐비트가 결정되도록 하는 것입니다. 두 과정은 큐비트의 파동 함수를 조작함으로써 이루어집니다.

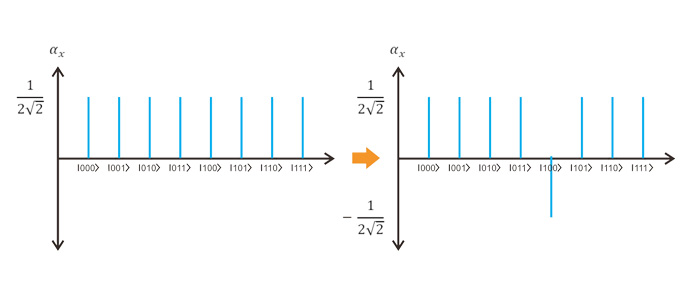
오라클 과정에 대해 자세히 살펴봅시다. 오라클 과정은 찾아내고자 하는 상태만의 진폭을 반전시키는 과정입니다. 아래 그림의 막대는 큐비트의 진폭을 표현한 것으로 진폭의 제곱이 해당 상태가 관측될 확률을 의미하며 막대가 x축 대칭이 되는 것은 해당 상태의 진폭이 반전되었다는 의미입니다. 위 그림에서 각 상태의 관측 확률은 1/8이고 오라클 과정 이후 진폭이 반전된 ∣100⟩이 찾고자 하는 상태인 것입니다.

여기서, 오라클 과정은 '관측'이 아닌가? 어떻게 찾으려는 상태의 진폭만 반전시킬 수 있지? 라는 궁금증이 들 것입니다. 양자 붕괴가 일어나지 않는 이유는 오라클 과정이 가역적인 연산이기 때문입니다. 가역적인 연산은 간단히 역함수가 존재하는 연산으로 이해할 수 있습니다. 즉, 입력과 출력이 일대일 대응이 되어 정보의 손실이 일어나지 않는 연산인 것입니다. 이는 앞서 살펴본 큐비트의 비결정론적 성질과 연관되는데, 큐비트의 비결정론적 상태에 가역적 연산을 시행하더라도 언제든 되돌릴 수 있기 때문에 오라클 과정은 양자 붕괴를 일으키지 않는 것입니다. 오라클 과정은 큐비트의 모든 상태에 대해 하나의 가역적인 연산을 하지만, 찾으려는 정답 상태의 진폭만을 반전시킵니다.

이렇게 찾으려는 상태의 진폭을 반전시키더라도 진폭의 제곱의 값은 아직 1/8로 추가적인 과정이 필요한데요. 바로 그로버 알고리즘의 핵심인 평균 진폭 반사(Inversion about average) 과정입니다.

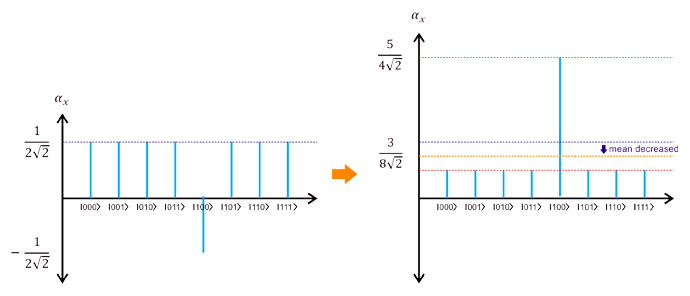
평균 진폭 반사 과정은 정답 상태의 확률을 증폭시키는 데 핵심 역할을 합니다. 정답 상태의 진폭만을 반전시키면, 이는 다른 상태와 비교했을 때 평균 진폭에서 더 멀어진 값(음수 측)으로 치우치게 됩니다. 이제 '평균 진폭을 기준으로 대칭이 되도록' 연산을 하면, 음수 방향으로 크게 벗어나 있던 정답 후보는 양수 쪽으로 큰 폭의 도약을 하게 되고 다른 상태의 진폭은 조금 작아지게 됩니다. 결과적으로 정답 후보 진폭이 크게 증폭되어, 관측 시 큐비트가 정답 상태로 결정될 확률이 높아집니다.

이 과정을 여러 차례 반복한 후 마지막에 관측하면, 높은 확률로 정답 비밀번호를 얻을 수 있습니다. n개의 중첩 수에 대해 그로버 연산 과정을 √n 번 반복하면 충분히 높은 확률로 정답 상태를 얻을 수 있음이 알려져 있기 때문에 기존 컴퓨터로 10000번이 걸릴 문제를 100번 내외 연산으로 해결할 수 있게 되는 셈입니다.

그런데 "평균 진폭을 기준으로 반사"와 같은 연산이 어떻게 모든 큐비트에 대해 정확히 이루어질 수 있을까요? 바로 얽힘(Entanglement)을 이용하기 때문입니다.

얽힘(Entanglement)ⁱⁱ⁾

중첩이 단일 큐비트 내부의 현상이라면, 얽힘은 두 개 이상의 큐비트가 긴밀히 연결되어, 하나의 큐비트를 관측하면 다른 큐비트의 상태도 즉시 결정되는 양자역학적 현상을 말합니다. 이때 중요한 점은 두 큐비트가 각자 독립적으로 '0 또는 1'만을 갖는 것이 아닌, 서로 양자 중첩 상태 전체를 공유하며 연산이 진행된다는 점입니다. 여러 큐비트를 얽힘 상태로 만들어 전체 양자 컴퓨터 시스템이 하나의 단위처럼 작동할 수 있도록 할 수 있습니다.

정답 탐색(검색)을 위한 그로버 알고리즘 외에도 양자 어닐링⁴⁾이나 양자 자기 최적화⁵⁾와 같은 방법들이 양자 붕괴를 피하며 최적해를 구하기 위해 활용됩니다. 하지만 양자 컴퓨터의 완전한 구현을 위해 해결해야 할 중요한 과제가 남아 있습니다. 바로 '오류 정정'입니다.

양자 오류 정정(Quantum Error Correction)의 중요성

양자 붕괴 문제와 함께 넘어야 할 또 하나의 장애물은 오류 발생입니다. 기존 컴퓨터에서 오류 발생은 온도·전자기파·우주 방사선 등의 외부 요인에 의해 비트의 상태가 바뀌는 것을 말합니다. 오류가 발생하면 저장해둔 데이터 비트의 상태가 바뀌거나, 정보통신 시 송수신 과정에서 비트의 상태가 바뀌어 본래 송신한 정보와 다른 내용이 수신되는 문제가 발생합니다.

큐비트가 너무 민감하기 때문에 외부 요인에 의해 상태가 쉽게 바뀌거나 왜곡될 수 있어 오류 발생에 더욱 치명적입니다. 또한 양자 컴퓨터에서는 얽힘을 사용하기에 큐비트의 하나의 상태가 바뀌면 얽혀 있는 다른 큐비트의 상태에도 영향을 주게 되어 한 번의 작은 오류라도 계산 과정이 반복되면서 전체 결과에 큰 영향을 미칠 수 있습니다. 따라서 양자 컴퓨터에서는 오류 정정(Error Correction) 기술이 필수적입니다.

패리티 비트

양자 오류 정정 기술을 이해하기 위해 기존 컴퓨터의 대표적인 오류 정정 방식인 '패리티 비트(Parity Bit)'에 대해 살펴봅시다.

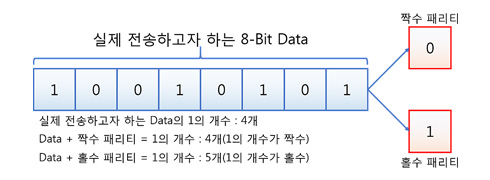
이 방법은 전송할 데이터 비트에 한 개의 보조 비트를 추가하여, 데이터 전체에 포함된 '1'의 개수가 짝수 혹은 홀수가 되도록 하여 오류 발생 여부를 확인할 수 있도록 합니다. 짝수 패리티(Even Parity) 방식을 위 그림에 적용하면 데이터가 총 8비트이고, 그 8비트 중 1의 총 개수가 4개로 짝수이기 때문에 패리티 비트를 0으로 설정해 1의 개수가 짝수가 되도록 맞추게 됩니다. 그러면 수신 측에서 전체 비트(8비트 + 패리티 비트)를 확인하여 1의 개수가 홀수인 경우 오류가 발생하였음을 확인하고 송신 측에 다시 정보 전달을 요청합니다. 재송신 요청을 받은 경우 송신 측은 복사해둔 전체 비트를 재송신합니다.

오류가 발생한 위치를 찾거나, 2개 이상의 비트에서 동시에 오류가 발생한 경우를 위해서는 더 고도화된 방식이 필요하지만 "데이터 외에 추가 정보를 보내, 오류 여부를 파악하고 오류 발생 시 송신을 다시 요청한다."라는 오류 정정의 기본 개념을 확인할 수 있습니다.

물리적 큐비트, 논리적 큐비트?

하지만 양자 오류 정정은 더 까다롭습니다. 고전 데이터는 언제든 복제해 두었다가 오류가 생기면 다시 송신하거나 백업할 수 있지만, 양자역학에는 데이터 복제를 위해 큐비트를 확인하는 순간 양자 붕괴가 일어나게 됩니다. '복제 불가능 정리(No-Cloning Theorem)'에 따라 큐비트 상태를 그대로 복사할 수 없다는 것이 알려져 있습니다. 또한 비트의 상태가 0에서 1로, 1에서 0으로 바뀌는 비트 오류만 존재하는 고전 컴퓨터와 달리, 양자 컴퓨터에서는 파동 함수의 위상이 바뀌는 위상 오류에 대한 오류 정정도 이루어져야 합니다.

양자 오류 정정의 핵심은 여러 개의 물리적 큐비트를 얽힘을 통해 하나의 논리적 큐비트로 구성하는 것입니다. 물리적 큐비트는 실제 양자 컴퓨터 하드웨어에서 작동하는 개별적인 큐비트로, 외부 간섭에 의해 쉽게 오류가 발생할 수 있습니다. 반면 논리적 큐비트는 여러 물리적 큐비트로 구성되어 오류를 감지하고 수정할 수 있는 안정적인 단위입니다. 큐비트 복제는 불가능하지만 여러 물리적 큐비트를 통해 큐비트의 정보를 분산하여 저장하는 논리적 큐비트를 만들어 오류 정정을 진행합니다.

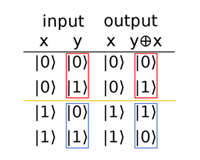
논리적 큐비트를 구성하기 위해 CNOT 게이트가 사용됩니다. CNOT 게이트는 양자 게이트 중 하나로 2개의 큐비트를 받아 2개의 큐비트를 반환합니다. CNOT 게이트는 제어 큐비트의 상태가 1일 경우 타겟 큐비트의 상태를 바꾸는 역할을 합니다. 제어 큐비트의 상태는 변하지 않고, 제어 큐비트가 1일 경우에만 타겟 큐비트의 상태를 변화시키는 것입니다.

이때 CNOT 게이트의 타겟 큐비트로 ∣0⟩을 넣으면 제어 큐비트와 타겟 큐비트의 상태가 항상 같게 됩니다. 즉, 타겟 큐비트에 제어 큐비트의 정보를 분산할 수 있는 것입니다. 위 그림에서 Y가 0인 경우 항상 두 큐비트의 결과 상태가 같다는 점을 이용하는 것입니다.

양자 오류 정정은 기본적으로 위와 같은 원리로 정보를 분산하여 다수결 원칙을 통해 오류를 감지하고 수정하는 반복 코드(Repetition Code) 방식이 있습니다. 3가지 큐비트에 정보를 분산하여 1개의 큐비트에 오류가 생기더라도 2개의 큐비트가 표현하는 상태를 통해 오류를 감지하는 방식입니다. 간단한 구현 방식으로 초기 양자 컴퓨터의 이론 연구에 활용되었으나 물리적 큐비트가 많이 소모되고, 정보가 저장되는 효율이 낮은 문제가 있습니다.

따라서 더 정확한 오류 위치 감지, 실시간 오류 수정 등을 위해 표면 코드(Surface Code), 색 코드(Color Code) 등의 오류 정정 알고리즘이 연구되고 있습니다. 이 중에서 최근 발표된 구글의 윌로우 칩의 경우 표면 코드 방식을 사용합니다.

구글 윌로우(Willow) 칩

2024년 발표된 구글의 윌로우(Willow) 칩이 많은 관심을 받게 된 이유도 양자 오류 정정 기술에서 뛰어난 발전이 있었기 때문입니다. 연구팀은 2D 격자 구조를 기반으로 한 표면 코드(Surface Code) 방식의 양자 오류 정정 기술을 사용하여 오류율을 상용화를 위한 임계값 이하로 유지하는 데 성공하였습니다.

표면 코드에 대해 이해하기 위해 먼저 쇼어 코드(Shor Code)에 대해 살펴봅시다. 양자 컴퓨터 초기 양자 오류 정정 기술로 제시된 쇼어 코드는 9개의 물리적 큐비트로 하나의 논리적 큐비트를 구성하여 비트, 위상 오류를 감지하고 수정하는 방식입니다. 그러나 1D의 선형 구조를 가져서 9개의 물리적 큐비트가 모두 하나의 논리적 큐비트의 오류 감지와 수정을 위해서 쓰이기 때문에 효율이 좋지 않았습니다.

그러나 2D 격자 구조의 표면 코드는 다수의 관측 큐비트(Measure qubit)가 인접한 데이터 큐비트(Data qubit) 다수를 보호하는 시스템으로 더 적은 큐비트로 양자 오류 정정을 진행할 수 있습니다. 또한 격자 구조의 배치이기 때문에 실리콘 기반의 초전도체 양자 칩에 쉽게 적용할 수 있고, 그 확장이 용이하다는 장점이 있습니다.

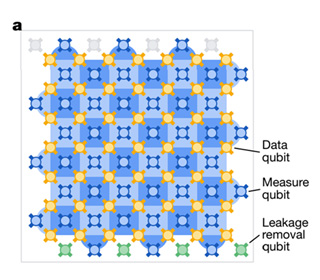
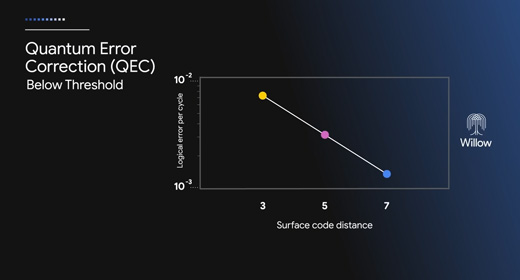
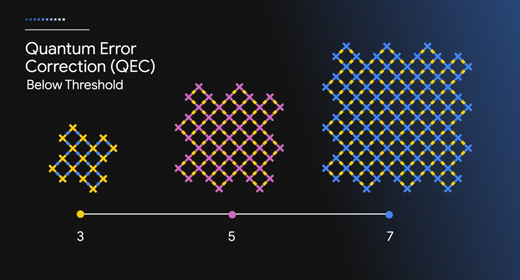
윌로우 칩이 주목받은 이유는 큐비트 수가 증가할수록 오류율이 안정된다는 점에 있습니다. 양자 오류 정정 기술에서 중요한 사실은 바로 오류를 관측하고 수정할 때 쓰이는 큐비트, 윌로우 칩의 경우 관측 큐비트 자체도 오류가 발생할 수 있다는 점입니다. 이로 인해 큐비트 수를 늘림에 따라 오류 정정 효과가 증가함에도 여러 오류가 누적되어 오류율이 크게 증가하는 문제점이 있었고, 이것이 큐비트 확장을 통한 양자 컴퓨터 상용화에 큰 걸림돌이었습니다.

윌로우 칩은 실시간 디코딩 기법(Real-time Decoding) 기술을 통해 오류 감지 후 수정까지 속도를 향상시켜 오류 확산을 방지했습니다. 또한 측정 큐비트의 신뢰도를 높이는 보정 알고리즘을 적용하여, 오류 탐지 과정에서 발생하는 추가적인 오류를 줄이는 데 성공했습니다.

양자 컴퓨터, 미래를 만들다.

오늘은 양자 컴퓨터의 기본 원리와 구현 방식, 그리고 양자 컴퓨터 기술의 핵심인 양자 오류 정정 기술까지 함께 살펴보았습니다. 양자 컴퓨터는 신약 개발, 분자 시뮬레이션, 인공지능 학습, 금융 포트폴리오 최적화 등 첨단 산업 전반에 혁신을 가져올 국가 핵심 기술로 주목받고 있습니다.

양자 컴퓨터는 아직 많은 기술 발전을 필요로 하여 상용화까지 시간이 필요합니다. 상용화까지 시간에 대해서 여러 예측이 존재하지만, 미래는 예측하기보다 만들어가는 것이라고 생각합니다. 새로운 미래를 만들어갈 예비 공학도 여러분들을 양자 컴퓨터의 세계로 초대합니다. 공학으로, 양자 컴퓨터로 미래를 이어갈 여러분을 응원하며 이번 기사는 여기서 마치겠습니다.